p/q-Formel: 4 Tipps zum Lösen quadratischer Gleichungen
Quadratische Gleichungen kann man auf unterschiedliche Arten und Weisen lösen. Der einfachste Weg ist sicherlich die Anwendung der p/q-Formel. Ich zeige dir in diesem Text übersichtlich und leicht verständlich, wie du bei quadratischen Gleichungen die pq-Formel – manchmal auch PQ-Formel oder PQ-Formel geschrieben – anwenden kannst und worauf du besonders aufpassen musst.
Da die p/q-Formel ein wichtiges Hilfsmittel bei der Lösung quadratischer Gleichungen ist, solltest du sie am besten auswendig lernen. So sieht sie aus:
Im Folgenden besprechen wir ausführlich, welche Arbeitsschritte notwendig sind, um die p/q-Formel anzuwenden und welche Fehler immer mal wieder von Schülern in Schulaufgaben gemacht werden. Du bekommst außerdem wertvolle Tipps, wie du diese Fehler in Zukunft vermeiden kannst.
p/q-Formel: Einige Grundlagen, die du für die Anwendung benötigst
Ein Fallbeispiel
In einer Klassenarbeit hast du folgende quadratische Gleichung gegeben:
x² – 6x + 5 = 0
Diese Gleichung kannst du jetzt mit der pq-Formel lösen. Und das geht so:
Als erstes musst du p und q finden. Dabei ist p immer die Zahl, die vor dem x steht und q ist die Zahl ohne x.
x² – 6x + 5 = 0 => p = -6
x² – 6x + 5 =0 => q = 5
(Vorsicht: Du musst das Vorzeichen mit beachten.)
Wenn du p und q bestimmt hast, setzt du diese in die Lösungsformel von oben ein.
Achte darauf, alle Minuszeichen abzuschreiben. Zwei davon kommen aus der Formel und das vor p darfst du natürlich auch nicht vergessen. Vor der Wurzel ist dir bestimmt schon aufgefallen, dass da ein PLUS über einem MINUS steht. Deshalb jetzt der folgende Schritt:
Schreibe dir die Formel zweimal ab, einmal mit PLUS und einmal mit MINUS. Je nachdem, wie gut du im Kopfrechnen bist, kannst du hier auch schon alles in den Taschenrechner eingeben und ausrechnen lassen.
x1 = 5 und x2 = 1 sind also die Lösungen unserer Gleichung.
Kann ich die p/q-Formel immer verwenden?
Die pq-Formel kannst du immer anwenden, wenn vor dem x² kein Koeffizient oder eine „1“ steht.
Und wenn vor dem x² doch ein anderer Koeffizient als die „1“ steht?
In dem Fall teilst du einfach die ganze Gleichung durch diesen Koeffizient. An der Lösung der Gleichung ändert das nichts und du kannst die p/q-Formel verwenden. Allerdings sind dann p und q manchmal nicht mehr ganz so einfach.
Und wenn es kein p oder kein q gibt?
Dann ist p oder q halt NULL. Die pq-Formel funktioniert deswegen trotzdem noch. Allerdings gibt es dann einfachere Wege, um an die Lösungen zu kommen. Ist q = 0, so kannst du p einfach auf die andere Seite bringen und durch einfaches Wurzelziehen deine Lösungen erhalten. Ist p hingegen NULL, so lässt sich ein x ausklammern.
Erklärvideos und Übungen zum Ausklammern sowie zum Umstellen von Gleichungen kannst du auf der Seite LEARNZEPT.de finden.
Wenn du damit aber unsicher bist, kannst du immer die p/q-Formel benutzen.
Liefert die p/q-Formel immer meine Lösungen?
Ja, aber du musst aufpassen. Denn eine quadratische Gleichung hat nicht immer Lösungen. Und wenn die quadratische Gleichung keine Lösung hat, kann dir die pq-Formel auch keine liefern. Der Taschenrechner würde dann einen Fehler melden. Daher solltest du dir immer überlegen, wie viele Lösungen es überhaupt gibt.
Das kannst du mit einer Skizze machen, oder aber in dem du die Diskriminante berechnest.
Was ist die Diskriminante?
Die Diskriminante „D“ ist das, was in der p/q-Formel unter der Wurzel steht.
Wenn D > 0, dann gibt es zwei Lösungen.
Wenn D < 0, dann gibt es keine Lösung der quadratischen Gleichung, denn aus einer negativen Zahl kannst du keine Wurzel ziehen.
Ein besonderer Fall tritt ein, wenn D = 0 ist. Dann hast du genau eine Lösung.
Diese Aussagen über die Diskriminante stimmen übrigens auch für eine andere Lösungsformel für quadratische Gleichungen, nämlich die Mitternachtsformel. Erklärvideos und Übungsaufgaben dazu findst du auf LEARNZEPT.de.
p/q-Formel: Das sind die häufigsten Fehler in Klassenarbeiten!
- Um die p/q-Formel verwenden zu können, muss das x² einen Koeffizienten von eins haben. Es darf also vor dem x² nur eine „1“ oder gar nichts stehen.
Ist der Koeffizient vor dem x² nicht „1“, musst du erst die gesamte Gleichung durch diesen Koeffizienten teilen.
- p ist der Koeffizient vor dem x, q die Zahl ohne x. Verwechsle das bitte nicht.
Das hat auch erstmal nichts mit der Reihenfolge der Summanden zu tun. Allerdings ist es üblich, eine Gleichung so aufzuschreiben, dass q als letzter Summand in der Gleichung steht.
p/q-Formel: Mit 4 Tipps zur richtigen Lösung
Die p/q-Formel ist wirklich einfach. Arbeite einfach die folgenden vier Schritte ab:
1) Die quadratische Gleichung Normieren! Normieren heißt durch den Koeffizienten vor dem x² teilen. Dieser ist danach dann „1“. Das ist wichtig, weil sonst die pq-Formel nicht anwendbar ist.
2) Einfach p und q aus der Gleichung ablesen.
3) Werte für p und q in die Formel einsetzen. Hier ist sie nochmal zur Ansicht:
4) Die Formel mit den Werten für p und q einmal für PLUS und einmal für MINUS in den Taschenrechner eingeben und die Ergebnisse aufschreiben.
p/q-Formel: Hier bekommst du Hilfestellung
Benötigst du weiterführende, übersichtliche Erklärungen zum Thema p/q-Formel? Bist du auf der Suche nach weiterem Übungsmaterial?
Die Online-Lernplattform LEARNZEPT bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.

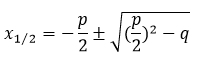
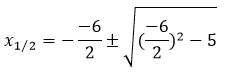
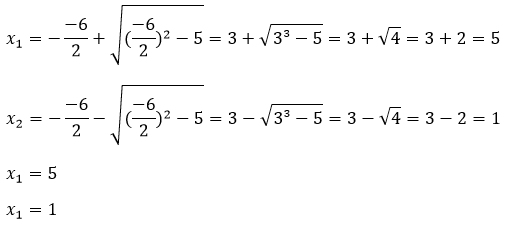


 (25 Bewertung/en, durchschnittlich: 3,52 von 5)
(25 Bewertung/en, durchschnittlich: 3,52 von 5)
Entschuldigung, Kommentare zu diesem Artikel sind nicht möglich.