Bruchterme addieren: 2 Tipps zum Brüche zusammenzählen

Wie addiert man Bruchterme und muss das wirklich so schwer sein? In diesem Text wirst du lernen, wie du Bruchterme addierst. Du wirst lernen wie du den gemeinsamen Hauptnenner findest, die beiden Bruchterme auf den gleichen Nenner erweiterst, und so die beiden Bruchterme einfach addieren kannst.
Das Bruchterme addieren ist nur dann schwer, wenn man keine Zwischenschritte macht und das Ergebnis irgendwie sofort angeben möchte. Wir werden aber Schritt für Schritt vorgehen. Auf diese Art und Weise wirst du das Bruchterme addieren auch verstehen. Versprohen!
Wir gehen in den folgenden Arbeitsschritten vor:
- Hauptnenner finden
- Brüche auf den Hauptnenner erweitern
- Alles auf einen Bruchstrich mit dem Hauptnenner im Nenner schreiben
- Zähler und Nenner so weit wie möglich vereinfachen
Bruchterme addieren: Erklärvideo
In diesem Video wird dir ausführlich erklärt wie du die Bruchterme addieren kannst.
Bruchterme addieren: Welche Techniken musst du dafür beherrschen?
Wie bereits erwähnt, kannst du Brüche erst dann addieren, wenn du den Hauptnenner bildest. Zunächst stellt sich also die Frage, wie du den Hauptnenner findest. Es werden jeweils zwei gleiche Faktoren aus beiden Nennern zusammengefasst, alle anderen Faktoren werden einfach übernommen. Jeder Faktor aus beiden Nennern muss einmal im Hauptnenner vorkommen.
Ausführliche Erklärungen, wie du bei Brüchen den Hauptnenner findest, gibt’s auf der Seite LEARNZEPT.de.
Beispiel:
Im den Nennern hast du die Faktoren „2“, „(x-2)“, „3“, „(x-2)“.
„(x-2)“ kommt doppelt vor. Wir brauchen jeden Faktor aber nur einmal. Daher haben wir als Hauptnenner „2•3•(x-2)“
Du siehst, dem ersten Bruchterm fehlt als Faktor nur die „3“. Wir erweitern ihn daher mit „3“. Dem zweiten Bruchterm fehlt als Faktor die „2“, so dass wir mit „2“ erweitern müssen.
Und du erinnerst dich, beim Erweitern müssen Zähler und Nenner mit demselben multipliziert werden.
Genauere Erklärungen zum Erweitern von Brüchen findest du auf der Seite LEARNZEPT.de.
Du erkennst, der Nenner ist gleich und du kannst die beiden Brüche auf einen Bruchstrich schreiben.
Nun ja Zähler und Nenner kannst du jetzt noch vereinfachen:
Wie kann ich Bruchterme addieren, wenn meine Nenner nicht nur aus Faktoren bestehen sondern aus einer Summe oder einer Differenz?
Du meinst wie diesem Beispiel?
Hier bleibt dir keine Wahl und du musst „faktorisieren“, also versuchen möglichst viel auszuklammern.
Im ersten Bruchterm kannst du „4x“ ausklammern und erhältst als Nenner: 4x•(1+2x).
Du siehst sofort, „(1+2x)“ kommt im ersten Bruch einmal vor und im zweiten Bruch zweimal. Jeweils ein Vorkommen können wir zusammenfassen. Es bleiben die Faktoren „4x“, „(1+2x)“ und „(1+2x)“. Der Hauptnenner ist also 4x∙(1+2x)2.
Dem ersten Bruch fehlt also einmal der Faktor „(1+2x)“ und dem zweiten „4x“. Du musst also entsprechend erweitern:
Da der Nenner jetzt gleich ist, schreibst du beide Zähler auf einen Bruchstrich und erhältst:
Das Faktorisieren von Termen kannst du ausgiebig auf der Seite LEARNZEPT.de wiederholen und üben.
Bruchterme addieren: Häufige Fehler, die immer wieder passieren
- Um die Zähler auf einen Nenner zu schreiben, müssen die Nenner gleich sein. Sonst geht das nicht!
- Sind die Nenner nicht gleich, und bestehen aus einer Summe oder einer Differenz musst du zuerst faktorisieren. Häufig kannst du dafür einfach ausklammern.
Bruchterme addieren: 2 Tipps zum richtigen Zusammenzählen
- Finde den Hauptnenner und erweitere deine Brüche entsprechend. Schreibe dann beide auf einen Nenner und vereinfache.
- Besteht einer deiner Nenner aus einer Summe oder einer Differenz, dann musst du faktorisieren.
Bruchterme addieren: Hier bekommst du Hilfestellung
Benötigst du weiterführende, übersichtliche Erklärungen zum Thema Bruchterme addieren? Bist du auf der Suche nach weiterem Übungsmaterial?
Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.


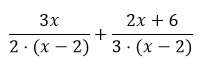
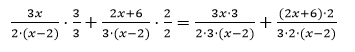
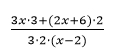
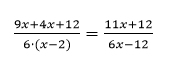


Entschuldigung, Kommentare zu diesem Artikel sind nicht möglich.