Nebenwinkel: 2 Tipps zum Berechnen von Winkeln

Winkel werden in der Geometrie zur Berechnung unbekannter Winkel in geometrischen Figuren oft zueinander in Beziehung gesetzt. Ein solcher typ von Winkeln, die sich zueinander in Beziehung setzen lassen sind die sogenannten Nebenwinkel. Diese Nebenwinkel haben bestimmte Eigenschaften, die bei der Berechnung anderer Winkel helfen, und sie sind sehr einfach in geometrischen Figuren erkennbar. Im Folgenden Text werde ich dir die Eigenschaften der Nebenwinkel anhand von Bildern so übersichtlich erklären, dass du danach damit in Klassenarbeiten keine Probleme mehr haben wirst.

Nebenwinkel finden sich immer an zwei Geraden, die sich schneiden. Wie der Name schon sagt, sind es die beiden Winkel, die am Schnittpunkt der beiden Geraden nebeneinander liegen. Folgende Skizze zeigt dir, wie ein mögliches Bild aussehen kann, bei dem du die Nebenwinkel anwenden kannst.

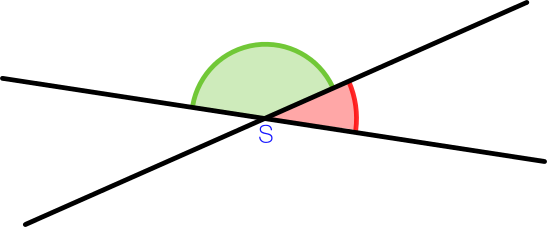
Zwei Geraden schneiden sich in einem Punkt S. Die beiden farbigen Winkel sind Nebenwinkel.

Nebenwinkel und ihre speziellen Eigenschaften

Wenn sich zwei Geraden schneiden:

Nebenwinkel entstehen an den Schnittpunkten, an denen zwei Geraden sich schneiden. Oben im Bild kannst du erkennen, dass ich von den beiden Winkeln sprechen, die nebeneinander liegen. Zum besseren Verständnis zeichnen wir uns noch einmal die obige Skizze ab und tragen die Winkel ein.

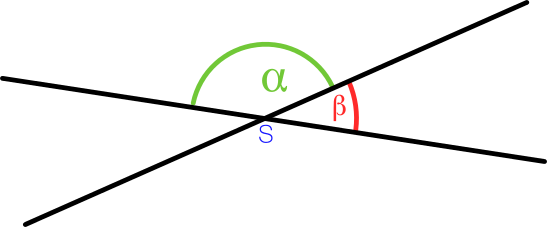
Die besondere Eigenschaft von Nebenwinkeln ist, dass sie, wenn man sie zusammenzählt immer genau 180° ergeben.

Mathematisch ausgedrückt heißt dies:

$\alpha \quad + \quad \beta \quad = \quad 180^{\circ}$

Die beiden Nebenwinkel ergeben also zusammen immer die Winkelsumme 180°.

Zur Winkelsumme an Geraden oder in geometrischen Flächen oder Körpern findest du ausführliche Erklärungen unter LEARNZEPT.de.

Wenn zwei parallele Geraden von einer dritten Geraden geschnitten werden:

Dass zwei Nebenwinkel zusammen immer 180° ergeben, ist auch dann hilfreich, wenn zwei parallele Geraden von einer dritten Geraden geschnitten werden. Schau dir das folgende Bild an, dann siehst du, was ich damit meine:

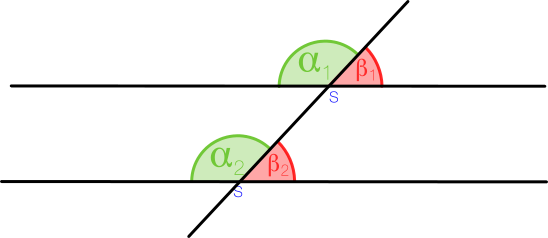
Hier gibt es jetzt zwei Schnittpunkte, an denen wir Nebenwinkel erkennen können.

Wie du siehst, sind die Nebenwinkel an beiden Schnittpunkten eingezeichnet. Die Winkelsumme der Nebenwinkel ist an beiden Schnittpunkten gleich. Aufgrund dieser Tatsache kannst du also feststellen, dass für beide Winkelpaare gilt:

$\alpha_{1} \quad + \quad \beta_{1} \quad = \quad 180^{\circ}$

$\alpha_{2} \quad + \quad \beta_{2} \quad = \quad 180^{\circ}$

Außer den Nebenwinkeln gibt es noch andere Winkelarten, die in der Geometrie sehr hilfreich sein können. Diese Winkel (Scheitel-, Wechsel- und Stufenwinkel) kannst du dir auf der Seite LEARNZEPT.de ausführlich erklären lassen.

Achtung: Nebenwinkel und ihre Fehlerquellen?

Du hast bestimmt schon einmal in einer Klassenarbeit erlebt, dass du eine Aufgabe nicht lösen konntest und nach der Korrektur der Lehrer neunmalklug festgestellt hat, dass du ja NUR die Nebenwinkel erkennen hättest müssen.

Meine Unterrichtserfahrung zeigt jedoch, dass es für Schüler oft eben nicht so einfach ist, die Nebenwinkel zu erkennen. Einige Erkennungsmerkmale findest du hier:

Wir benötigen zwei Geraden, die sich schneiden, oder zwei parallele Geraden, die von einer dritten Geraden geschnitten werden.
Am Schnittpunkt der beiden Geraden oder an den beiden Schnittpunkten bei zwei parallelen Geraden ergeben die Winkel, die nebeneinander liegen zusammen immer 180°.
Diese Winkel nennt man dann Nebenwinkel.

Mein Tipp: Schau dir bei ähnlichen Aufgaben immer genau an, ob zwei Winkel an Schnittpunkten nebeneinander gemeinsam eine Gerade ergeben. Sie sind dann Nebenwinkel und ergeben zusammen genau 180°.

Erkennen und berechnen von Nebenwinkeln in 2 Tipps

Schau dir die angegebene Zeichnung genau an, speziell die Winkel, die nebeneinander liegen.
Wenn du keine Zeichnung gegeben hast, dann mach dir eine Skizze.
Nebenwinkel liegen, wie der Name sagt, nebeneinander und ergeben zusammen 180°.

Nebenwinkel: Hier bekommst du Hilfestellung

Wie wäre es, wenn du die Eigenschaften der Nebenwinkel und ihre Verwendung übersichtlich und leicht verständlich wiederholen könntest? Möchtest du mit echten Klassenarbeiten und ausführlichen Erklärungen und Lösungen auf die nächste Prüfung lernen?

Erklärvideos und echte, interaktiv aufbereitete Klassenarbeiten zur Übung gibt’s nur auf der Online-Lernplattform Learnzept! Klicke hier für einen kostenlosen Account!

(3 Bewertung/en, durchschnittlich: 2,33 von 5)