Flächeninhaltsformel Dreieck: 5 Tipps zur Berechnung

Den Flächeninhalt von Dreiecken berechnen, das ist zunächst mal kein mathematisches Thema, das Schülern die Schweißperlen auf die Stirn treibt. Da gibt es doch bestimmt eine Formel dafür. In die braucht man dann nur die gegebenen Werte einsetzen und schon hat man das Ergebnis. Ehrlich gesagt, recht viel komplizierter ist es auch nicht. In diesem Text werde ich dir dennoch ausführlich aber verständlich erklären, wie die Flächeninhaltsformel für ein Dreieck aussieht und welche Größen du benötigst, um sie anzuwenden.

Natürlich weißt du, was ein Dreieck ist und wie ein Dreieck aussieht. Sehen wir uns trotzdem mal eines an, damit wir auch sicher über den gleichen Gegenstand sprechen.

Von einer Figur wie dieser wollen wir jetzt die Fläche bestimmen. Wir kramen einmal im Gedächtnis und erinnern uns, dass wir dafür eine Grundlinie und eine Höhe benötigen. Außerdem war da in der Formel noch das Problem, dass wir irgendetwas durch 2 teilen mussten.

Aber der Reihe nach. Sieh dir zunächst einmal das folgende Erklärvideo genauer an. Danach kannst du entscheiden, ob du noch Erklärungsbedarf hast. Wenn ja, lies einfach weiter. Ich werde dir in einer verständlichen Sprache ohne unnötige Fachbegriffe erklären, wie du die Flächeninhaltsformel im Dreieck anwenden kannst und besonders auch, welche Fehler meiner Unterrichtserfahrung nach häufig in Klassenarbeiten auftreten und wie du sie vermeiden kannst. Du siehst, es lohnt sich weiterzulesen.

 

Flächeninhaltsformel Dreieck: Erklärvideo

In diesem Video wird dir erklärt, wie du die Flächeninhaltsformel von Dreiecken richtig anwendest.

 

 

 

Flächeninhaltsformel Dreieck: Grundlagen zur Anwendung

Welche Größen und Strecken gibt es in einem Dreieck?

Erste, nicht ganz ernst gemeinte Antwort: Nicht viele. Schau dir mal die folgende Skizze an:

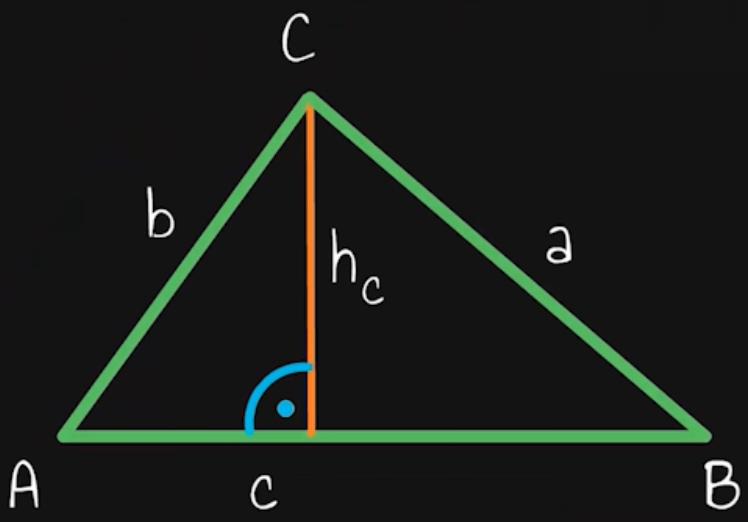
Um die Flächeninhaltsformel für Dreiecke anwenden zu können, benötigen wir folgende Strecken. Zunächst einmal brauchen wir eine Grundlinie g (in unserer Skizze die Strecke c zwischen den Eckpunkten A und B). Außerdem brauchen wir eine Höhe h. Diese ist in unserer Skizze orange eingezeichnet. Wichtig ist, dass die Höhe h senkrecht auf der Grundlinie g steht. Das erkennst du an dem blau eingezeichneten rechten Winkel. Außerdem muss die Höhe durch den Eckpunkt des Dreiecks gehen, der gegenüber der Grundlinie liegt. Praktischerweise wird für diesen Punkt der gleiche Buchstabe verwendet wie für die Grundlinie, nämlich C.

Sind diese Punkte gegeben, dann kannst du die Flächeninhaltsformel für Dreiecke anwenden.

Wie lautet denn nun die Flächeninhaltsformel für Dreiecke?

Machen wirs kurz. Ich schreibe dir die Formel jetzt gleich mal auf und verliere dann noch ein paar Worte dazu.

Flächeninhaltsformel Dreieck:

Um den Flächeninhalt eines Dreiecks zu berechnen nehmen wir als die Grundlinie g mal die dazugehörige Höhe h und teilen das Ergebnis durch 2.

Wenn wir also unsere Strecken, wie oben schon erklärt, gefunden haben, dann brauchen wir nur in die Formel einzusetzen. Das ist tatsächlich einfach.

Der Einfachheit halbe sollten wir die Formel vielleicht gleich noch umstellen, es könnte ja schließlich sein, dass wir das Volumen in einer Aufgabe gegeben haben und die Grundlinie oder die Höhe berechnen sollen.

Formel für die Grundlinie g:

Formel für die Höhe h:

Das Umstellen von Formeln aller Art kannst du übrigens bequem auch anhand von Erklärvideos und echten Klassenarbeiten auf der Seite LEARNZEPT.de üben.

Gibt es Spezialfälle?

Na klar gibt es die. Die gibt es doch immer. Wäre ja sonst auch langweilig. Bei der Flächeninhaltsformel für Dreiecke heißen die Spezialfälle Rechtwinklige Dreiecke. Warum sind Rechtwinklige Dreiecke ein Spezialfall. Schauen wir uns zunächst eine Skizze an:

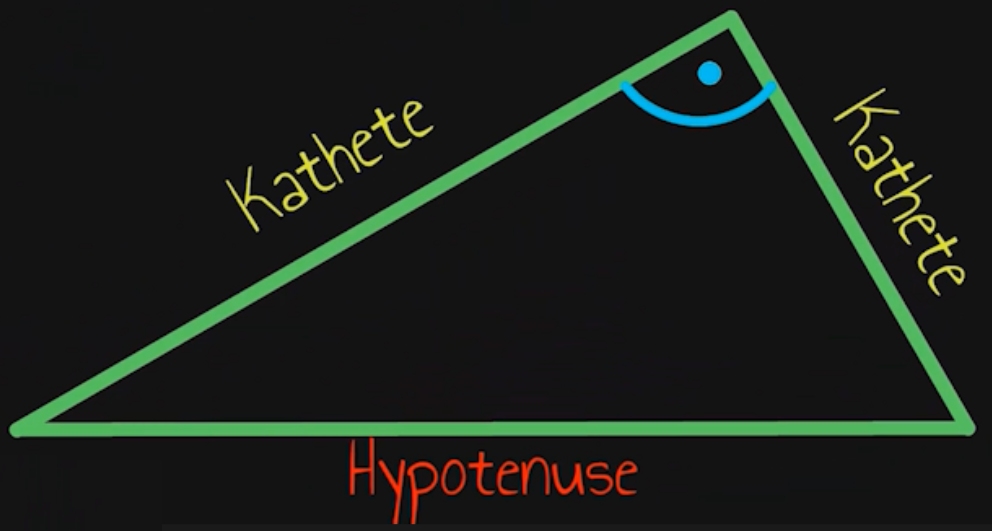
Zunächst stellen wir fest, dass es im rechtwinkligen Dreieck eine Hypotenuse und zwei Katheten gibt. Diese leiten sich aus dem Satz des Pythagoras her, den man im rechtwinkligen Dreieck verwenden kann. Genauere Informationen mit Erklärvideos und echten Klassenarbeiten findest du auf der Seite LEARNZEPT.de.

Wir stellen außerdem fest, dass die beiden Katheten zueinander senkrecht sind. Wir erkennen dies am blau eingezeichneten rechten Winkel. Für uns heißt das, wir haben unsere Höhe und unsere Grundlinie für die Flächeninhaltsformel von Dreiecken bereits gefunden, nämlich die beiden Katheten. Drehen wir das Dreieck einmal, dann wird es deutlicher:

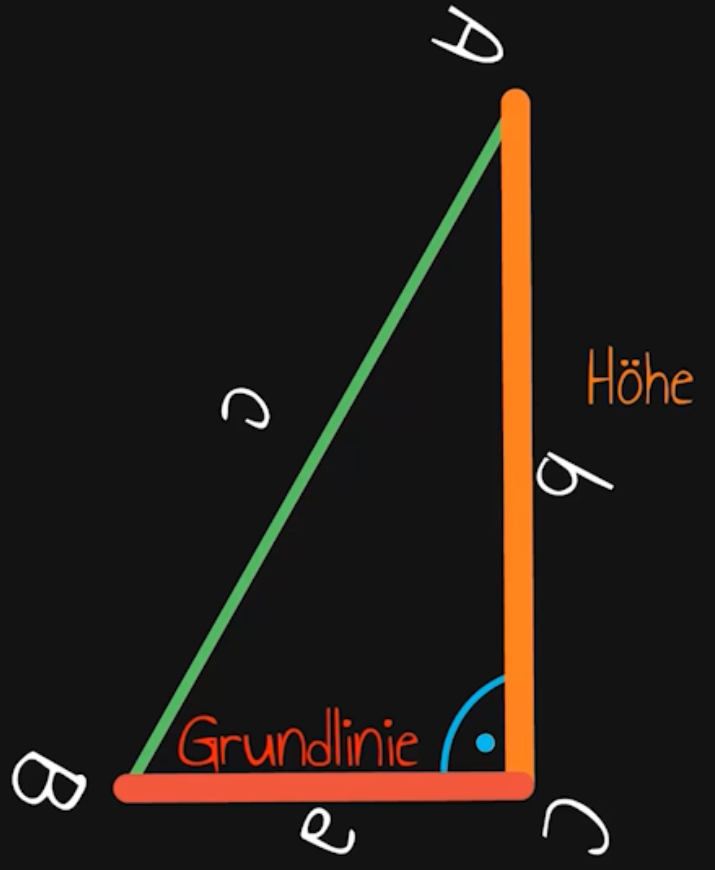
Jetzt sieht unser Dreieck von eben wieder so aus, wie wir es gewöhnt sind, nämlich die Grundlinie liegt unten und senkrecht darauf steht die Höhe. Jetzt ist uns klar, dass wir die beiden Katheten in die Flächenformel einsetzen müssen, um den Flächeninhalt unseres Dreiecks zu erhalten.

 

Flächeninhaltsformel Dreieck: Wo steckt der Fehlerteufel?

Bei der Anwendung der Flächeninhaltsformel beim Dreieck machen Schüler in Klassenarbeiten eigentlich nur einen groben Fehler immer wieder, nämlich die richtigen Strecken (Grundlinie und Höhe) in die Formel einzusetzen. Sehen wir uns noch einmal eine zusammenfassende Skizze an:

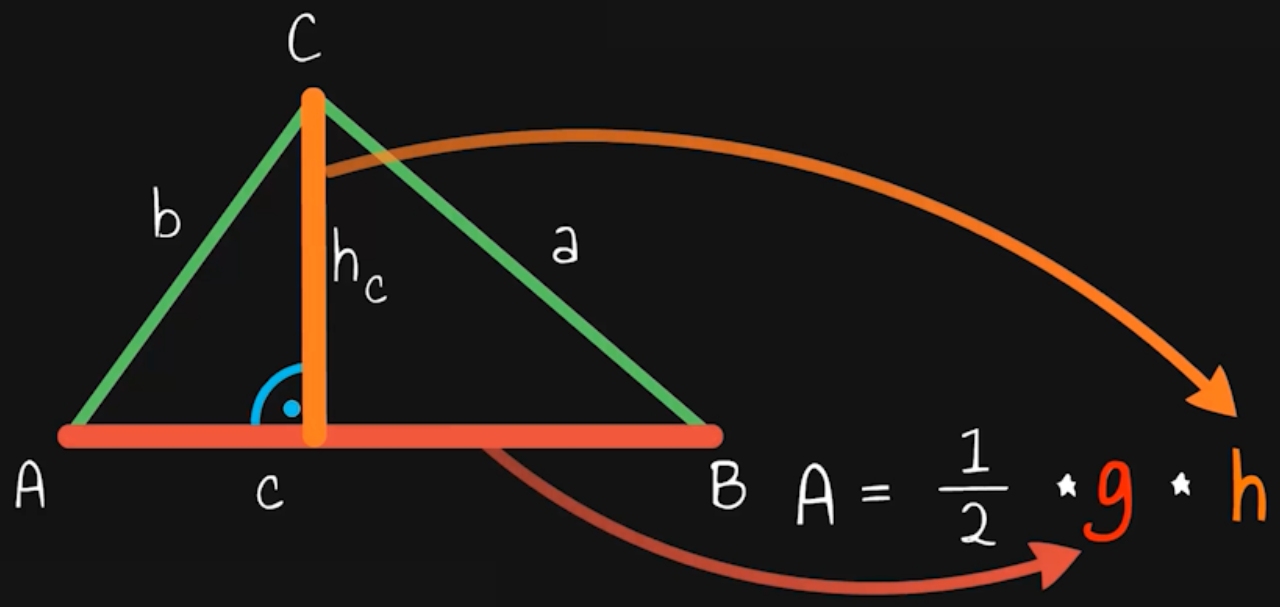
Für die Flächeninhaltsformel eines Dreiecks benötigen wir die Grundlinie und die Höhe, die senkrecht, also in einem 90-Grad-Winkel auf ihr steht und durch den gegenüberliegenden Eckpunkt des Dreiecks geht. Andere Strecken zur Berechnung des Volumens darfst du nicht verwenden. (Also, verwenden kannst du sie schon, aber das Ergebnis ist dann halt falsch und es gibt auf die Aufgabe keine Punkte.) Leider passiert dies in Klassenarbeiten meiner Unterrichtserfahrung nach oft.

Mein Tipp: Wie immer bei geometrischen Aufgaben hilft auch hier eine ordentliche beschriftete Skizze. Wenn du die Strecken vor dir liegen hast, dann brauchst du nur noch die Bedingungen, die wir gerade festgehalten haben, bezüglich der Grundlinie und der Höhe beachten und es kann nichts mehr schief gehen.

Bedenke den Spezialfall der rechtwinkligen Dreiecke! Bei rechtwinkligen Dreiecken sind die beiden Katheten bereits Grundlinie und Höhe, da sie zueinander senkrecht stehen.

Mein Tipp: So doof es klingt, aber drehe in der Klassenarbeit ruhig dein Angabenblatt einmal, so dass du das gegebene Dreieck aus mehreren Blickwinkeln betrachten kannst und mache das Gleiche mit einer Skizze. So fällt dir ein möglicher 90-Grad-Winkel nämlich besser auf.

 

Flächeninhaltsformel Dreieck: In 5 Schritten zum richtigen Flächeninhalt

1. Sieh dir die gegebene Figur genau an oder zeichne dir eine Skizze!

2. Trage die angegebenen Maße in deine Skizze ein! (Achte auf gleiche Benennungen und Maßeinheiten!)

3. Bestimme Grundlinie und Höhe in deinem Dreieck! (Suche den 90-Grad-Winkel, den du für die Höhe brauchst!)

4. Setze die gegebenen Werte in deine Formel ein!
(Sieh dir die Formel und die Umstellungen noch einmal oben an und lerne sie auswendig! So schwer ist die Formel nicht!)

5. Überprüfe dein Ergebnis!
(Hast du die richtige Benennung? Flächeninhalte geben wir mit „hoch 2“ oder „quadrat“ an!)

 

Flächeninhaltsformel Dreieck: Hier gibt’s Hilfestellung

Wie wäre es, wenn du das Thema Flächeninhaltsformel Dreieck übersichtlich und leicht verständlich wiederholen könntest? Möchtest du mit echten Klassenarbeiten und ausführlichen Erklärungen und Lösungen auf die nächste Prüfung lernen?

Erklärvideos und echte, interaktiv aufbereitete Klassenarbeiten zur Übung gibt’s nur auf der Online-Lernplattform Learnzept! Klicke hier für einen kostenlosen Account!

(8 Bewertung/en, durchschnittlich: 3,38 von 5)
Loading...