Besondere Dreiecke: 4 Tipps wie du sie immer erkennst

Was ein Dreieck ist, und wie man seine Fläche berechnet, das weißt du bereits. Hier möchte ich deine Aufmerksamkeit auf 4 besondere Dreiecke lenken, deren Eigenschaften beim Berechnen der Fläche helfen und die häufig in Klassenarbeiten abgeprüft werden.

Die 4 besonderen Dreiecke, die Gegenstand dieses Textes sind, sind:

1. Rechtwinklige Dreiecke
2. Gleichschenklige Dreiecke
3. Gleichseitige Dreiecke
4. Gleichschenklig rechtwinklige Dreiecke

Besondere Dreiecke sind deswegen wichtig, weil sie besondere Eigenschaften haben. Was für eine tolle Information, denkst du dir jetzt bestimmt. Allerdings ist es dir eine große Hilfe, wenn du dir diese Eigenschaften einmal speziell ansiehst. In Klassenarbeiten sind nämlich oft besondere Dreiecke versteckt und es wird vorausgesetzt, dass du ihre Eigenschaften kennst. Wenn du sie aber nicht kennst, dann kommst du bei den Aufgaben irgendwann an einem Punkt an, an dem du nicht mehr weiterrechnen kannst.

Es lohnt sich also für dich, die Eigenschaften von besonderen Dreiecken einmal richtig zu lernen. Hast du sie einmal verstanden, dann verlierst du in Klassenarbeiten nicht unnötig Punkte.

Ich werde dir die Eigenschaften genau erklären und dich auch auf spezielle Fehlerquellen hinweisen, die Schülern meiner Erfahrung nach immer wieder unterlaufen.

Besondere Dreiecke: Erklärvideo

Besondere Dreiecke: Gibt es ein spezielles Grundwissen?

Wie bereits erwähnt haben besondere Dreiecke besondere Eigenschaften, die du kennen musst, um bestimmte Aufgaben in Klassenarbeiten lösen zu können. Außerdem keine Sorge! Die Eigenschaften sind unkompliziert und einfach zu erklären.

Machen wir uns einfach eine Liste der 4 besonderen Dreiecke und sehen wir uns ihre Eigenschaften genau an.

1. Rechtwinklige Dreiecke:

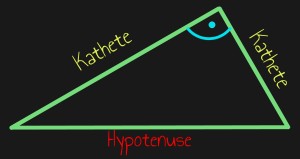
Rechtwinklige Dreiecke sind besondere Dreiecke, weil sie einen rechten Winkel haben. Ein rechter Winkel hat 90 Grad und ist dann im Dreieck aufgrund der Winkelsumme (180 Grad) immer der größte Winkel im Dreieck. Genaueres zur Winkelsumme in Dreiecken findest du auf LEARNZEPT.de. Die Seite, die dem rechten Winkel gegenüberliegt wird auch Hypotenuse genannt. Sie ist auch die längste Seite. Die beiden kürzeren Seiten sind die Schenkel des rechten Winkels und werden auch Katheten genannt.

 

2. Gleichschenklige Dreiecke:

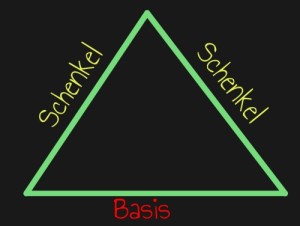
Gleichschenklige Dreiecke sind besondere Dreiecke, weil sie zwei Seiten (= Schenkel) haben, die gleich lang sind. Dies heißt außerdem, dass an den beiden Schenkeln zwei gleichgroße Winkel anliegen, die sogenannten Basiswinkel. Die Basis zu den Basiswinkeln ist zudem die Seite, die keinen gleichlangen Partner hat. Wiederum aufgrund der Winkelsumme im Dreieck lässt sich der Winkel so berechnen:

Dritter Winkel = 180 Grad – Beide Basiswinkel

 

3. Gleichseitige Dreiecke:

Im gleichseitigen Dreieck sind alle drei Seiten gleich lang und außerdem alle drei Winkel gleich groß, nämlich genau 60 Grad.

 

4. Gleichschenklig rechtwinklige Dreiecke:

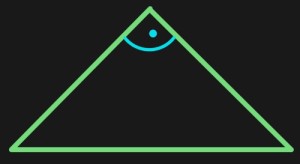
Gleichschenklig rechtwinklige Dreiecke sind deswegen besondere Dreiecke, weil sie, genau wie gleichschenklige Dreiecke auch, zwei gleichlange Seiten haben. Diese beiden gleichlangen Seiten sind immer die Schenkel eines rechten Winkels. Die beiden anderen Winkel müssen, weil sie Basiswinkel sind, gleich groß sein und deshalb 45 Grad haben. Übrigens, dein Geodreieck ist genau ein solches Dreieck. Am Geodreieck kannst du dir alle Eigenschaften ansehen.

Das war’s auch schon. Mehr besondere Dreiecke gibt es nicht. Zumindest sind sie für dich in Klassenarbeiten nicht wichtig. Wie du unkompliziert die Fläche von Dreiecken berechnen kannst, findest du auf LEARNZEPT.de.

 

Besondere Dreiecke: Häufige Fehler, die es zu vermeiden gilt

Fehler entstehen meiner Unterrichtserfahrung nach erstens immer dann, wenn Schüler besondere Dreiecke in Klassenarbeiten nicht als solche erkennen.

Mein Tipp:

Genau einprägen, wie besondere Dreiecke jeweils aussehen und dann prüfen, ob die Figur in der Aufgabe besondere Dreiecke enthalten. Besondere Dreiecke können in verschiedenen Positionen in einer Aufgabe verwendet werden, außerdem können sie auch gedreht werden.

Fehler entstehen zweitens dann, wenn der Schüler besondere Dreiecke in der Aufgabe zwar erkennt, jedoch ihre Besonderheiten nicht kennt.

Mein Tipp:

Auswendig lernen, welche Eigenschaften besondere Dreiecke haben und diese dann in der Aufgabe auch anwenden!

 

Besondere Dreiecke: Zusammenfassende Tipps

Es gibt folgende besondere Dreiecke:

1. Rechtwinklige Dreiecke: Einer der drei Winkel im Dreieck hat 90 Grad. Weitere Eigenschaften habe ich oben bereits erwähnt.
2. Gleichschenklige Dreiecke: Zwei Seiten des Dreiecks sind gleich lang. In der Erklärung weiter oben findest du noch andere Eigenschaften
3. Gleichseitige Dreiecke: Alle Seiten sind gleich lang und alle Winkel sind gleich groß (60 Grad).
4. Gleichschenklig rechtwinklige Dreiecke: Denke einfach an dein Geodreieck. Zusätzliche Erklärungen findest du weiter oben im Text.

 

Besondere Dreiecke: Hier bekommst du Hilfestellung

Benötigst du weiterführende, übersichtliche Erklärungen zum Thema besondere Dreiecke? Bist du auf der Suche nach weiterem Übungsmaterial?
Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.

(14 Bewertung/en, durchschnittlich: 4,14 von 5)

Loading...

[/vc_column_text][/vc_column][/vc_row]