Logarithmusfunktion ableiten: 2 Tipps zur richtigen Ableitung

Wenn die Logarithmusfunktion doch immer nur ein ln(x) wäre. Dann wäre die Ableitung sehr sehr einfach. Wie sie geht und was du machst, wenn du z.B. die Ableitung von ln(x+5) finden sollst, lernst du hier. Außerdem lernst du, dass auch dann die Ableitung nicht schwer zu finden ist. Welche Fehler Schüler beim Ableiten der Logarithmusfunktion am häufigsten machen und wie du diese Fehlerquellen umschiffen kannst zeige ich dir ebenfalls in diesem Text.

Die Formel, mit der du die Logarithmusfunktion ableiten kannst, musst du dir einfach merken.

$f(x) \quad = \quad ln(x)$

$f'(x) \quad = \quad \frac{1}{x}$

Das ist leicht.

Allerdings ist die Logarithmusfunktion oft verkettet. Und die Kettenregel anzuwenden fällt nicht allen Schülern leicht. Du erinnerst dich: “Innere Ableitung mal äußere Ableitung“.

Beispiel:

$f(x) \quad = \quad ln(3x+2)$ Innere Ableitung = 3 $f'(x) \quad = \quad 3\cdot\ \frac{1}{(3x+2)}$

Du musst also „das Innere“ – also das (3x+2) in der Klammer – ableiten. Danach schreibst du einen Bruch. Als Zähler hast du immer eine „1“. Im Nenner musst du jetzt nur „das Innere“ (3x+2) hinschreiben.

Logarithmusfunktion ableiten: Erklärvideo

Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren

Video laden

YouTube immer entsperren

Logarithmusfunktion ableiten: Was muss ich wissen um die Logarithmusfunktion ableiten zu können?

$f(x) \quad = \quad ln(x)f'(x) \quad = \quad \frac{1}{x}$

Das musst du dir einfach erstmal merken!

Beispiele:

$f(x) \quad = \quad 4\cdot\ ln(x)$ Innere Ableitung = 1 $f'(x) \quad = \quad 4\cdot\ \frac{1}{x}$
$f(x) \quad = \quad ln(x+3)$ Innere Ableitung = 1 $f'(x) \quad = \quad \frac{1}{x+3}$
$f(x) \quad = \quad ln(4 x^{2}+2)$ Innere Ableitung = 8x $f'(x) \quad = \quad 8x \cdot \frac{1}{4x^{2}+2}$
$f(x) \quad = \quad ln(2x^{3}-5x^{2})$ Innere Ableitung = 6x²-10x $f'(x) \quad = \quad (6x^{2}-10x) \cdot \frac{1}{2x^{3}-5x^{2}}$
$f(x) \quad = \quad ln(sin(x))$ Innere Ableitung = $cos(x)$ $f'(x) \quad = \quad cos(x) \cdot \frac{1}{sin(x)}$
$f(x) \quad = \quad ln(3x \quad + \quad e^{x+5})$ Innere Ableitung = $3 \quad + \quad e^{x+5}$ $f'(x) \quad = \quad (3+ e^{x+5}) \quad \cdot \quad \frac{1}{3+ e^{x+5}}$

Wenn du dir die Funktionsterme der Ableitungen in dem Beispielen ansiehst erkennst du das sich viele noch weiter vereinfachen lassen. Fast immer können wir den Vorfaktor oder die Vorfaktoren als Zähler schreiben.

Und ja Brüche kann man Kürzen. Auch Brüche mit x. Aber Vorsicht : „Aus Differenzen und Summen kürzen nur die Dummen“. Aber das heißt nicht, dass nur weil der Nenner aus einer Summe bestehen wir nicht kürzen dürfen. Wir müssen aber zuerst ausklammern.

Wenn du die Regeln für das Ausklammern bei Termen oder das Kürzen von Brüchen wiederholen willst, dann kannst du dies auf der Seite LEARNZEPT.de ausgiebig tun.

Bei Beispiel 3 und 4 können wir noch kürzen.

Schau dir die Beispiele weiter an:

Hier kannst du erst die „zwei“ ausklammern und dann kürzen.

Bei diesem Beispiel siehst du, dass in jedem Summanden, sowohl im Zähler, als auch im Nenner ein x vorkommt. Dieses können wir daher ausklammern und kürzen.

Logarithmusfunktion ableiten: Häufige Fehler, die wir ab heute nicht mehr machen

Da die Ableitung des Logarithmus nicht gerade intuitiv ist, fällt es vielen Schülern schwer sich die Formel zu merken.

Mein Tipp: Lerne die Formel wie eine Vokabel: f'(x)=1/x

Wenn du die Standardlogarithmusfunktion ableiten kannst, die Formel also noch weißt, musst du nur noch wissen, wie du die Kettenregel anzuwenden hast und schon macht dir kein Logarithmus mehr Schwierigkeiten. Beim Ableiten der Logarithmusfunktion heißt das: Die Ableitung der Klammer in den Zähler, die Klammer selber in den Nenner.
Viele Schüler vergessen das Nachdifferenzieren, wenn sie die Logarithmusfunktion ableiten.
Bei welchen anderen Funktionen du außerdem beim Ableiten nachdifferenzieren musst, wird dir auf der Seite LEARNZEPT.de ausführlich erklärt.

Mein Tipp: Denk immer daran, mit der inneren Ableitung mal zu nehmen.

Logarithmusfunktion ableiten: Zwei Tipps zusammengefasst

Die Natürliche Logarithmusfunktion ableiten ist leicht, es gilt f'(x)=1/x.
Steht in der Klammer mehr wie ein x, so musst du mit der Regel „Innere Ableitung mal Äußere Ableitung“ arbeiten.

Logarithmusfunktion ableiten: Hier bekommst du Hilfestellung

Benötigst du weiterführende, übersichtliche Erklärungen zum Thema Logarithmusfunktion ableiten? Bist du auf der Suche nach weiterem Übungsmaterial?

Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.

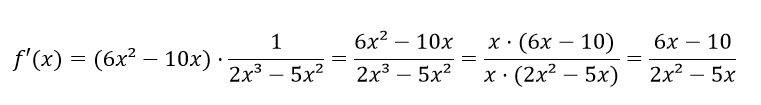
(10 Bewertung/en, durchschnittlich: 4,40 von 5)