Rechenregeln Logarithmus: 3 Tipps zur richtigen Berechnung

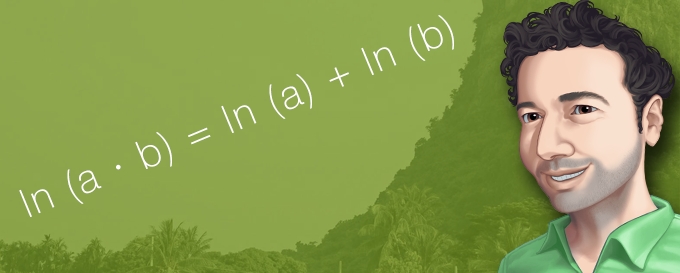
Rechenregeln Logarithmus

Was heute der Taschenrechner, war früher der Logarithmus: Das Hilfsmittel, um komplizierte Rechnungen zu vereinfachen. Ganze Bücher wurden nur mit Logarithmuswerten gefüllt. Wie konnte der Logarithmus die Rechnungen vereinfachen? Der Logarithmus hat eine beeindruckende Eigenschaft. Alles wird um eine Stufe leichter. Aus Mal wird Plus, aus Geteilt wird Minus, Potenzen werden zu Multiplikationen und Wurzeln zu Divisionen.

Und du weißt selber, dass es meistens leichter ist, zwei Zahlen zu addieren als zu multiplizieren, vor allem wenn sie groß sind. Mussten die Mathematiker beziehungsweise vor allem die Ingenieure zwei große Zahlen miteinander malnehmen, nutzen sie die erste Logarithmus Regel aus die besagt:

ln (a*b) = ln (a) + ln (b)

War man also an a*b interessiert, schlug man in der Logarithmentafel ln (a) und ln (b) nach, addierte die beiden Werte und fand das Ergebnis wieder in der Logarithmentafel.

Klingt kompliziert, war aber immer noch leichter, als zwei große Zahlen miteinander zu multiplizieren.

Rechenregeln Logarithmus: Was muss ich dafür können und wissen?

Der Logarithmus ist die Gegenoperation zum Potenzieren. Somit sind die Rechenregeln des Logarithmus das Gegenstück zu den Potenzregeln. Ausführliche Erklärungen zu den Potenzregeln und ausreichend Übungsmaterial gibt’s auf der Seite LEARNZEPT.de.

Der Logarithmus ist nur für positive reelle Zahlen definiert. Wenn ich vom Logarithmus spreche, sind alle Logarithmen gemeint, es sei denn es steht eine Basis direkt dabei. Denn die Regeln und Eigenschaften der Logarithmen unterschieden sich nicht.

Die Wichtigste Rechenregel beim Logarithmus ist die Lassoregel. Du brauchst die Lassoregel häufig, wenn du Exponentialgleichungen lösen willst. Nimm zum Beispiel die Gleichung 100^X=100.000. Um hier x zu berechnen, solltest du das x „Hinunterholen“.

Die Lassoregel besagt:

$log \quad a ^{b}= b\cdot log \quad a$

Für unser Beispiel bedeutet das:

$100 ^{x} = 100.000 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad | log$
$log \quad 100 ^{x} = log \quad 100.000$
$x \cdot log \quad 100 = log \quad 100.000 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad |log = 2$
$x \cdot 2 = 5 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad | :2$
$x = 2,5$

Weitere Rechenregeln:                    Beispiel:
$log \quad (a \cdot b) \quad = \quad log \quad a + log \quad b$                 $log \quad (100x) \quad = \quad log \quad 100 + log \quad x \quad = \quad 2 + log \quad x$
$log \quad \frac{a}{b} \quad = \quad log \quad a - log \quad b$                      $log \quad \quad \frac{x}{1000}\quad =\quad log\quad x-log\quad 1000\quad =\quad log\quad x-3$

Aus der Lassoregel lässt sich folgern:
$log \quad \sqrt[n]{a} \quad = \quad log \quad a ^{\frac{1}{n}} \quad = \quad \frac{log a}{n}$

Es lohnt sich einige Sonderfälle auswendig zu lernen:

$log \quad 1 \quad = \quad 0$
$log_{{a}} \quad a \quad = \quad 1$

Und da es immer noch Taschenrechner gibt, die nur den Zehnerlogarithmus und den ln beherrschen, hier die allgemeine Umrechnungsformel für den Logarithmus.

$log_{{b}} \quad (a) \quad = \quad \frac{log_{{c} \quad }a}{log_{{c} \quad }b}=\frac{log \quad a}{log \quad b}$

Rechenregeln Logarithmus: Problemstellungen, die zu häufigen Fehlern führen

Oft vermuten Schüler der Log(0) ist null. Das ist aber falsch.

Der Log(0) ist nicht definiert. Richtig ist Log(1)=0

Viele Schüler versuchen auch den Logarithmus fälschlich auseinander zu ziehen und machen aus Log(a+b)=Log(a)+Log(b). Das ist aber FALSCH. Diese Regel gibt es nur für ein Mal-Zeichen zwischen a und b, nicht aber für ein Plus-Zeichen.

Mein Tipp: Wende nur Rechenregeln an, die du auch tatsächlich gelernt hast. Alle anderen gibt es meistens nicht und deine Rechnung wird dann falsch.

Gerne wird auch übersehen, dass der Logarithmus nur für positive Zahlen definiert ist. Es gibt also einfach keinen Log(-2).

Mein Tipp: Merke dir einfach folgende Regeln:

Der Nenner eines Bruchs darf niemals null sein.
Unter der Wurzel darf keine negative Zahl stehen.
Beim Logarithmus gilt beides: Es gibt weder einen Logarithmus von der Null. Noch von negativen Zahlen.

Genauere Erklärungen zu diesen Regeln sowie zum Definitionsbereich des Logarithmus findest du auf LEARNZEPT.de.

Rechenregeln Logarithmus: Drei Tipps zusammengefasst

$log \quad x ^{n} \quad = \quad n \cdot log \quad x$ Durchs Logarithmieren wird also aus einer Potenz eine Multiplikation.
$log \quad (a \cdot b)\quad = \quad log \quad a +log \quad b$ Hier wird durchs Logarithmieren einer Multiplikation eine Addition.
Durch die Rechenregeln des Logarithmus vereinfachen sich also die Rechenoperationen.

Rechenregeln Logarithmus: Hier bekommst du Hilfestellung

Benötigst du weiterführende, übersichtliche Erklärungen zu den Rechenregeln des Logarithmus? Bist du auf der Suche nach weiterem Übungsmaterial?
Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.

1 Stern 2 Sterne 3 Sterne 4 Sterne 5 Sterne (18 Bewertung/en, durchschnittlich: 3,33 von 5)