Oberflächeninhalt Kegel: 3 Tipps zur perfekten Berechnung

Das Thema Oberflächeninhalt Kegel ist Teil der Raumgeometrie. Wie aber kannst du unkompliziert das Volumen von Kegeln berechnen? Welche Formeln benötigst du dazu? Wie und warum musst du in bestimmten Fällen den Satz des Pythagoras verwenden? Im Folgenden klären wir all diese Fragen. Ich werde dabei versuchen, dich, so gut es geht, nicht mit unnötigem Fachwortschatz verwirren, sondern dir die Berechnungsschritte so einfach und deutlich wie möglich zu erklären.

Zunächst sehen wir uns mal ein Beispiel für einen Kegel an:

Im wirklichen Leben begegnest du solchen Körpern zum Beispiel als Hütchen beim Sporttraining oder beim Straßenbau. Wie du siehst, ist ein Kegel ein spitzer Körper. Spitzer Körper heißt, er hat eine Grundfläche und eine Mantelfläche. Die Grundfläche ist immer ein Kreis. Wenn die Grundfläche kein Kreis ist, dann ist der Körper auch kein Kegel.

Die Oberfläche eines Kegels ist einfach zu berechnen, da sie nur aus zwei Teilflächen besteht, nämlich Mantel und Grundfläche. Also nicht verzagen, sondern erstmal das folgende Erklärvideo ansehen. Darin findest du eigentlich bereits alle Informationen, die du zur Berechnung des Oberflächeninhalt Kegel benötigst. Wenn du danach noch Fragen hast, beziehungsweise einen Leitfaden zur Vermeidung der häufigsten Fehler in Schulaufgaben möchtest, dann kannst du im Text einfach weiterlesen.

Oberflächeninhalt Kegel: Erklärvideo

In diesem Video erhältst du ausführliche Erklärungen zum Thema Oberflächeninhalt Kegel.

Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren

Video laden

YouTube immer entsperren

Oberflächeninhalt Kegel: Formeln und anderes Grundwissen für Klassenarbeiten

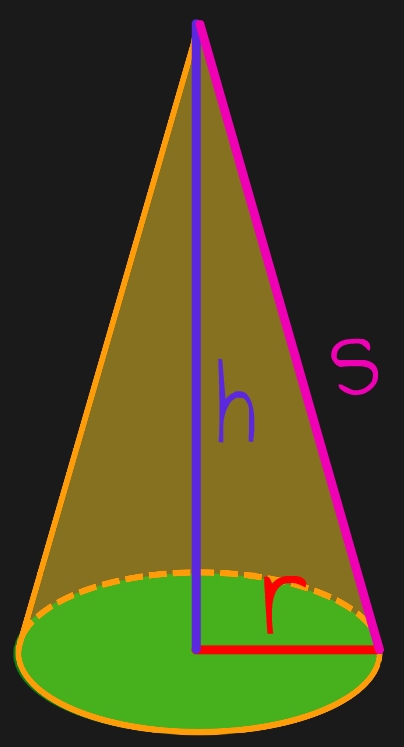
Sehen wir uns noch einmal ein Beispiel für einen Kegel an, diesmal jedoch mit ein paar zusätzlichen Details:

Wir wiederholen kurz, ein Kegel ist ein spitzer Körper. Spitzer Körper heißt, er besteht aus einer Grundfläche, nämlich immer einem Kreis und einer Matelfläche. Wenn man die beiden Flächen zusammenzählt erhält man die Oberfläche. Merke dir zum Anfang einfach folgende Formel:

$O \quad = \quad A_{{G}} \quad + \quad M$ (In Worten: Oberfläche = Grundfläche + Mantelfläche)

Das ist einfach zu merken. Lass uns deswegen ein wenig ins Detail einsteigen. Um wirklich zu mathematischen Formeln, mit denen du rechnen kannst, zu kommen sollten wir uns kurz mal ansehen, aus welchen Maßen so ein Kegel besteht.

Die Grundfläche ist, wie mehrfach schon gesagt, ein Kreis. So ein Kreis hat einen Radius „r“. Außerdem hat ein Kegel, wie jeder andere Körper auch, eine Höhe „h“. Diese geht von der Spitze senkrecht hinunter auf die Grundfläche. Da du es in der Schule nur mit sogenannten „geraden“ Kegeln zu tun hast, geht deine Kegelhöhe von der Spitze immer senkrecht auf den Mittelpunkt deiner Grundfläche.

Jetzt wird es schon ein bisschen spannender, denn so ein Kegel hat neben Radius und Körperhöhe noch die sogenannte Mantellinie „s“. Schau dir nochmal kurz in der Abbildung an, was mit dieser Mantellinie gemeint ist. Sie geht von der Spitze bis zu einem beliebigen Punkt außen an der Grundfläche.

Wir können die drei Strecken in folgenden Zusammenhang setzen:

r² + h² = s²

Die drei Linien bilden nämlich ein rechtwinkliges Dreieck und können daher über den Lehrsatz des Pythagoras ins Verhältnis gesetzt werden. Die Mantellinie ist dabei immer die längste Seite und deshalb immer die Hypotenuse dieses rechtwinkligen Dreiecks. (Für grundlegende Erklärungen und Übungen zum Lehrsatz des Pythagoras siehe LEARNZEPT.de.)

Lass uns kurz ein paar Formeln aufschreiben, mit denen du die Oberfläche des Kegels berechnen kannst.

Elementar ist erstmal die Formel für die Grundfläche. Die Grundfläche ist ein Kreis und Fläche Kreis geht immer so:

$A_{{G}} \quad = \quad r^{2} \quad \cdot \quad \pi$

Die Mantelfläche berechnest du folgendermaßen:

$M \quad = \quad r \quad \cdot \quad s \quad \cdot \quad \pi$ (In Worten: Mantelfläche = Radius • Mantellinie • π)

Jetzt finden wir auch noch eine allgemeine Formel für die Berechnung der Oberfläche zum Auswendiglernen:

$O \quad = \quad r \quad \cdot \quad \pi \quad \cdot \quad (r \quad + \quad s)$

Das wars auch schon. Jetzt hast du das gesamte Rüstzeug um die Oberfläche jedes Kegels auszurechnen.

Oberflächeninhalt Kegel: Wo kannst du typische Rechenfehler begehen?

1. Der erste Fehler, der in Klassenarbeiten immer wieder auftaucht ist, dass Schüler die Kreisfläche falsch berechnen. Die Flächenformel für die Kreisfläche lautet folgendermaßen:

$A_{{G}} \quad = \quad r^{2} \quad \cdot \quad \pi$

Diese Formel bitte nicht mit der Formel für den Kreisumfang verwechseln. (Siehe zur Flächenberechnung am Kreis auch LEARNZEPT.de.)

Mein Tipp: Jede Formel, die du verwendest, bitte genau ansehen, ob es auch die richtige ist. Die Kreisfläche ist eine beliebte Fehlerquelle, wenn es einmal schnell gehen muss.

2. Auch die zweite Fehlerquelle passiert im Eifer des Gefechtes schon einmal. Bitte verwende nicht die Körperhöhe zur Berechnung der Mantelfläche. Wenn die Mantellinie nicht gegeben ist, sondern nur die Körperhöhe, dann musst du die Mantellinie mithilfe des Satzes des Pythagoras (siehe auch LEARNZEPT.de) berechnen.

Mein Tipp: Wie immer an dieser Stelle und an ähnlichen Stellen bei anderen geometrischen Körpern empfehle ich dir dringend eine saubere Skizze anzufertigen und diese zu beschriften. Dann siehst du nämlich genau vor dir, was du gegeben hast und was du berechnen musst!

3. Die dritte immer wiederkehrende Fehlerquelle ist nach meiner Unterrichtserfahrung, dass Schüler oft mit Benennungen rechnen, die nicht homogen sind. Du kannst im metrischen System nur mit gleichen Benennungen rechnen, weil du sonst Äpfel mit Birnen vergleichst.

Mein Tipp: Beschrifte die Skizze, die du dir ohnehin immer machen solltest gleich mit gleichen Benennungen. Suche dir eine Einheit heraus, zum Beispiel Zentimeter und rechen andere Einheiten wie Meter oder Millimeter dann dementsprechend um.

Oberflächeninhalt Kegel: 3 Schritte zur richtigen Berechnung der Oberfläche

Mache dir immer eine sauber beschriftete Skizze. Achte darauf, was du an Maßen gegeben hast und rechne immer mit gleichen Maßen!
Pass auf, welche Formeln du verwendest. Besonders der Kreis ist mit Fläche und Umfang etwas trickreich.
Überprüfe dein Ergebnis, ob es stimmen kann. (Flächen geben wir in Quadrat an! „Hoch 2“ ist unverzichtbar.

Oberflächeninhalt Kegel: Hier bekommst du Hilfestellung

Gibt dir das Thema Oberflächeninhalt Kegel noch Rätsel auf?

Möchtest du Stift und Papier gegen interaktive und spannende Übungsaufgaben tauschen?
Die Online-Lernplattform Learnzept bereitet dich mit ausführlichen Erklärvideos und echten, interaktiv aufbereiteten Klassenarbeiten perfekt auf deine nächste Prüfung vor. Klicke hier für einen kostenlosen Account!

(1 Bewertung/en, durchschnittlich: 5,00 von 5)
Loading...

Schlagworte-Archive: Oberflächeninhalt Kegel