Bruchgleichungen lösen: 4 einfache Tipps als Leitfaden

Was ist eine Bruchgleichung? Wie löse ich Bruchgleichungen und worauf muss ich achten? Hier erfährst du, was Bruchgleichungen sind. Du lernst, wie du Bruchgleichungen löst, wie du vorgehen und worauf du achten musst. Du lernst außerdem, wie du die Definitionsmenge bestimmst und wie du anschließend die Bruchgleichung in eine normale Gleichung umformen kannst.
Haben wir eine Gleichung mit bei der x auch mal im Nenner vorkommt sprechen wir von einer Bruchgleichung.
Beispiel:
Im Folgenden werde ich dir erklären, wie du so eine Bruchgleichung am einfachsten lösen kannst und dich in einem weiteren Schritt mit einer Anzahl von Fehlerquellen vertraut machen, über die Schüler beim Bruchgleichungen lösen immer wieder stolpern.
Sieh dir zunächst einmal das folgende Video zum Thema Bruchgleichungen lösen an. Wenn du danach noch Fragen hast, dann lies einfach den Text weiter.
Bruchgleichungen lösen: Erklärvideo
In diesem Video wird dir ausführlich erklärt wie du Bruchgleichungen ganz unproblematisch lösen kannst.
Bruchgleichungen lösen: Wie ist die Vorgehensweise und welches Grundwissen benötigst du?
Wie löse ich eine Bruchgleichung?
Grundsätzlich musst du versuchen das x aus dem Nenner zu bekommen, damit du eine „normale“ Gleichung hast, die du ja bereits lösen kannst. Wie du bereits weißt, darfst du eine Gleichung nicht mit „0“ multiplizieren oder durch „0“ teilen. Hier ist also Vorsicht geboten. Um nicht jedesmal aufpassen zu müssen, ist es am einfachsten, vorher die Definitionsmenge zu bestimmen. So schließt du die „gefährlichen“ Situationen von vornherein aus. Anschließend beseitigst du die Nenner, indem du die Gleichung mit eben jenen Nennern multiplizierst. Abschließend löst du diese Gleichung nach „x“ auf.
Am Ende darfst du nur nicht vergessen zu überprüfen, ob die Lösung in der Definitionsmenge enthalten ist.
Wie finde ich die Definitionsmenge?
Die Nenner dürfen nicht „0“ werden. Du würdest du ja sonst durch Null teilen, was du ja eben nicht darfst. Grundsätzlich sind alle rationalen Zahlen erlaubt, bis auf eben einige Ausnahmen, bei denen der Nenner „0“ werden würde.
Diese Stellen findest du, in dem du für jeden Nenner bestimmst, für welche x-Werte dieser „0“ wird. Meistens sind die Nenner einfach und du kannst die kritischen x-Werte sofort sehen.
Ist ein Nenner mal komplizierter musst du ihn als eigene Gleichung gleich Null setzen und die entstandene Gleichung nach x auflösen. Alle x-Werte, die du auf diese Art und Weise findest sind problematisch und du musst sie aus der Definitionsmenge ausschließen.
Beispiel:
Du siehst sofort, x darf nicht 0 sein, sonst macht der erste Nenner schon einmal Probleme.
Und dass x nicht -3 sein darf, das kannst du am zweiten Bruch auch schnell erkennen.
Aber was kannst du aus der rechten Seite der Gleichung folgern? Da setzt du am besten den Nenner gleich Null:
(3x+6)*4-12 = 0 |+12
(3x+6)*4 = 12 |:4
3x+6 = 3 |-6
3x = -3 |:3
x = -1
Damit wissen wir, dass die Zahlen 0, -3 und -1 für uns problematisch sind, wir müssen sie also aus den Rationalen Zahlen ausschließen. Damit erhalten wir folgende Definitionsmenge:
Wie mache ich jetzt weiter, wenn ich die Definitionsmenge gefunden habe?
Du beginnst die Gleichung nach „x“ aufzulösen. Dafür musst du als erstes die ganze Gleichung mit jedem Nenner multiplizieren. Wenn du das richtig machst, erhältst du eine „normale“ Gleichung ohne lästige Brüche. Diese löst du dann einfach nach „x“ auf.
In manchen Gleichungen musst du nicht mit allen Nennern multiplizieren, sondern kannst dir durch das Finden eines Hauptnenners behelfen. Wie du das machst, kannst du auf LEARNZEPT.de wiederholen und üben.
Aber Achtung: Nicht jede dieser Lösungen ist auch eine Lösung der Bruchgleichung. Die Lösung muss auch in der Definitionsmenge enthalten sein.
Beispiel:
Definitionsmenge:
Gleichung mit den beiden Nennern multiplizieren:
Prüfen ob 4 in der Definitionsmenge ist: Ja, ist enthalten! Damit ist „4“ auch die Lösung der Bruchgleichung.
Die Definitionsmenge kannst du mit zwei unterschiedlichen Schreibweisen angeben. Beide Schreibweisen und wann du welche verwendest, findest du selbstverständlich auf LEARNZEPT.de.
Mach ich das immer so? Oder gibt auch Tricks wie es manchmal leichter geht?
Ja, es gibt manchmal Situationen, in denen es einfacher geht. Stehen zum Beispiel rechts und links des „=“ ein Bruch mit einem vergleichsweise einfachen Zähler, so kann es sich für dich lohnen, den „Kehrwert“ zu bilden. Aus den Zählern machst du dann jeweils Nenner und aus den Nennern jeweils den Zähler. Gerade wenn die Zähler kein x enthalten, wird so aus einer Bruchgleichung eine normale Gleichung.
Bruchgleichungen lösen: Die häufigsten Fehler in Klassenarbeiten:
- Oft vergessen Schüler, die Definitionsmenge vorher zu bestimmen. Und weil das die Lehrer wissen, ist die scheinbare Lösung dann nicht in der Definitionsmenge der Aufgabe in einer Klassenarbeit enthalten. Mein Tipp: Bestimme also immer als erstes die Definitionsmenge und mach es den Lehrern nicht so leicht!
- Wenn du mit den Nennern multiplizierst, dann denk daran, dass du die ganze Gleichung damit malnehmen musst. Das heißt jeden Summanden auf beiden Seiten der Gleichung.
- Oft wird auch verwechselt, welche Zahlen in der Definitionsmenge sind. Die Zahlen in der geschweiften Klammer sind eben jene, die aus der Definitionsmenge ausgeschlossen wurden. Diese Zahlen gelten nicht als Lösung der Gleichung.
Bruchgleichungen lösen: Drei Tipps zusammengefasst
- Bestimme die Definitionsmenge.
Achte auch darauf, dass du die geforderte Schreibweise verwendest. Informiere dich darüber auch auf LEARNZEPT.de. - Beseitige die Nenner, in dem du die Gleichung mit diesen multiplizierst.
- Löse diese Gleichung wie du es bereits gelernt hast.
- Vergleiche die Lösung mit der Definitionsmenge. Nur Lösungen in der Definitionsmenge sind echte Lösungen. Der x wert darf also nicht ausgeschlossen worden sein.
Bruchgleichungen lösen: Hier bekommst du Hilfestellung
Benötigst du weiterführende, übersichtliche Erklärungen zum Thema Bruchgleichungen lösen? Bist du auf der Suche nach weiterem Übungsmaterial?
Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.


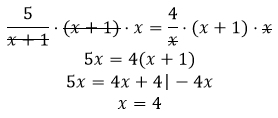


 (15 Bewertung/en, durchschnittlich: 3,53 von 5)
(15 Bewertung/en, durchschnittlich: 3,53 von 5)
Entschuldigung, Kommentare zu diesem Artikel sind nicht möglich.