Oberflächeninhalt Pyramide: 6 Tipps zur Berechnung

Das Thema Oberflächeninhalt Pyramide ist Teil des Fachgebietes der Raumgeometrie. Wie berechnet man aber unkompliziert das Volumen von Pyramiden? Welche Formeln brauchen wir dazu? Wann muss man mit dem Satz des Pythagoras arbeiten? All diese Fragen werden wir im Folgenden klären. Dabei versuche ich, so gut es geht, auf nervigen Fachwortschatz zu verzichten und die die Berechnungsschritte so einfach und deutlich wie möglich zu erklären.

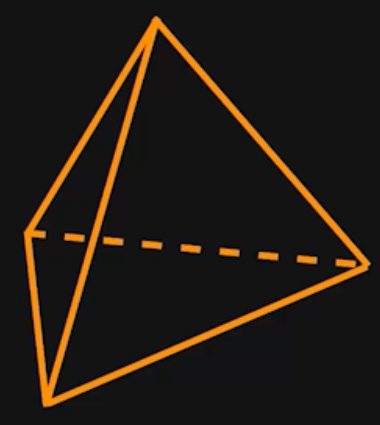
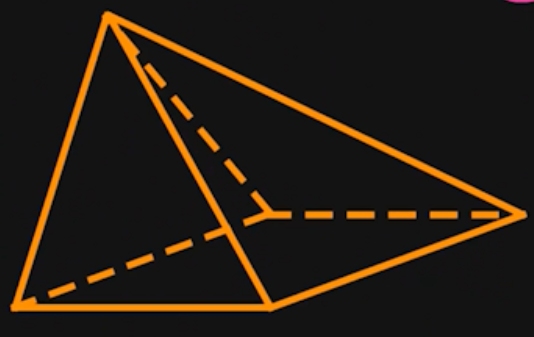
Sehen wir uns erstmal zwei Beispiel-Pyramiden an. Wie sieht eine Pyramide aus, und aus welchen Teilflächen besteht die Oberfläche einer Pyramide?

Eine Pyramide ist ein spitzer Körper. Spitzer Körper bedeutet, dass eine Pyramide eine Grundfläche besitzt und dreieckige Seitenflächen, die sich alle in einem Punkt über der Grundfläche treffen. Der Abstand zwischen diesem Punkt und der Grundfläche ist die Höhe der Pyramide. Die Höhe steht im 90-Grad Winkel auf der Grundfläche.

Die Oberfläche einer Pyramide besteht zum einen aus der Grundfläche. Diese kann ein Dreieck, ein Rechteck oder ein Quadrat sein. Außerdem hat eine Pyramide eine Mantelfläche. Sie besteht aus Dreiecken und zwar genau so vielen, wie die Grundfläche Ecken hat. Ein Dreieck als Grundfläche bedeutet also eine Mantelfläche mit drei Seitenflächen.

Zwei Formeln können wir festhalten:

$O \quad = \quad A_{{G}} \quad + \quad M$ (In Worten: Oberfläche = Grundfläche + Mantelfläche)

$M \quad = \quad A_{{1}} \quad + \quad A_{{2}} \quad + \quad A_{{3}} \quad + \quad ...$ (in Worten: Mantelfläche = Summe aller Seitenflächen)

Dies halten wir so erstmal fest. Schau dir jetzt das folgende Video an. Hier wird dir ausführlich erklärt, wie du die Oberfläche einer Pyramide am einfachsten berechnest. Wenn du danach noch Fragen haben solltest, dann erkläre ich dir die Berechnung des Volumens einer Pyramide noch einmal ausführlich aber ohne nervige Fachbegriffe und weise dich auch auf einige Fehler hin, die Schülern in Klassenarbeiten immer wieder unterlaufen.

Oberflächeninhalt Pyramide: Erklärvideo

In diesem Video erhältst du ausführliche Erklärungen zum Thema Oberflächeninhalt Pyramide.

Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren

Video laden

YouTube immer entsperren

Oberflächeninhalt Pyramide: Welche grundlegenden Lerninhalte musst du beherrschen?

Wie bereits gesagt ist eine Pyramide ein spitzer Körper. Welche Flächen musst du also berechnen, dass du die Oberfläche einer Pyramide erhältst. Zunächst musst du die Grundfläche berechnen. Davon gibt’s bei der Pyramide nur eine, wie wir ober bereits näher besprochen haben. Eine Pyramide kann aber unterschiedliche Grundflächen haben, zum Beispiel ein Dreieck, ein Rechteck oder ein Quadrat. Die Flächenformeln für diese Figuren kennst du ja ohnehin. Wir schreiben sie trotzdem noch einmal hin:

Dreieck: $A \quad = \quad \frac{1}{2} \quad \cdot \quad g \quad \cdot \quad h$

Rechteck: $A \quad = \quad a \quad \cdot \quad b \quad$

Quadrat: $A \quad = \quad a \quad \cdot \quad a \quad$

Wenn du die Berechnung der unterschiedlichen Flächen noch einmal wiederholen oder üben willst, kannst du das auf der Seite LEARNZEPT.de tun.

Wenn du die Grundfläche berechnet hast, dann kümmerst du dich um die Mantelfläche. Diese besteht aus so vielen Dreiecken, wie die Grundfläche Ecken hat. Wenn wir also als Beispiel eine rechteckige Grundfläche voraussetzen, dann hast du vier Dreiecke als Mantelfläche. Die Mantelfläche ist also nur die Summe der einzelnen Seitenflächen. Die Seitenflächen berechnest du natürlich mit der Flächenformel für Dreiecke. Diese findest du natürlich auch auf der Seite LEARNZEPT.de.

Dreieck: $A \quad = \quad \frac{1}{2} \quad \cdot \quad g \quad \cdot \quad h$

Um es dir etwas einfacher zu machen, normalerweise musst du gar nicht alle Seitenflächen einzeln ausrechnen.

Bei Pyramiden mit rechteckiger Grundfläche musst du dir genau ansehen, wo die Spitze der Pyramide liegt. Oft sind Seiten, die gegenüber liegen gleich groß, nämlich wenn die Spitze senkrecht über dem Mittelpunkt der Grundfläche liegt. Bei Pyramiden mit quadratischer Grundfläche sind dann sogar alle vier Seitenflächen gleich groß.

Bei Pyramiden mit dreieckiger Grundfläche hängt es stark von der Grundfläche ab. Am einfachsten ist hier die gleichseitige Pyramide. Bei solchen Pyramiden sind alle drei Seitenflächen gleich groß. Beim gleichschenkligen Dreieck sind zwei Seitenflächen gleich groß. Bei unregelmäßigen Dreiecken musst du genau hinsehen und alle drei Seitenflächen für sich berechnen.

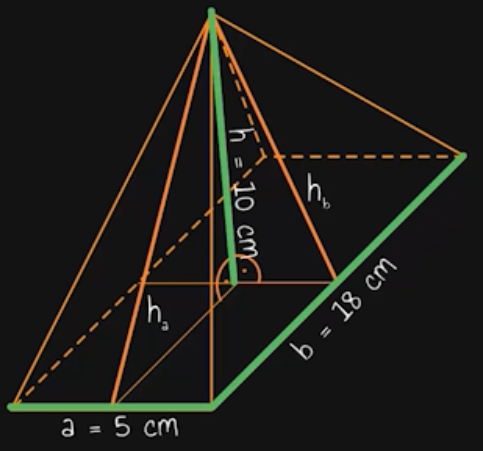
Aufpassen müssen wir mit der Höhe bei der Berechnung der Seitenfläche. In Pyramiden gibt es nämlich grundsätzlich zwei verschiedene Höhen. Zum einen gibt es die Seitenhöhe, nämlich die Höhe der einzelnen Seitenflächen. Zum anderen gibt es aber auch noch die Körperhöhe der Pyramide. Sie steht senkrecht auf der Grundfläche und führt bis zur Spitze. Oft musst du die Seitenhöhe mit Hilfe der Körperhöhe berechnen.

Dies funktioniert dann meistens mit dem Satz des Pythagoras. Dabei ist die Seitenhöhe immer die längste Seite des rechtwinkligen Dreiecks, das die Seitenhöhe, die Körperhöhe und die Grundlinie einschließen. Der Satz des Pythagoras lautet wie folgt:

$a^{2} \quad + \quad b^{2} \quad = \quad c^{2}$

Genauere Informationen zum Satz des Pythagoras sowie Tipps und Tricks, wie du am einfachsten mit dem Satz des Pythagoras rechnest, gibt’s auch auf LEARNZEPT.de.

So im Großen und Ganzen war es das eigentlich, was zur Berechnung der Oberfläche einer Pyramide zu sagen ist. Sehen wir uns im Folgenden ein paar typisch Fehler an, die Schülern immer wieder unterlaufen.

Oberflächeninhalt Pyramide: Wo stecken die wichtigsten Fehlerquellen?

1. Die erste Fehlerquelle ist dummerweise eigentlich dafür da, um dir Hilfestellung zu geben, nämlich die Formelsammlung. Pass auf, wenn du Formeln aus der Formelsammlung übernimmst. Diese Formeln sind meist sehr allgemein gehalten und bestimmte Teile von Formeln können in deiner gegebenen Figur aus der Klassenarbeit abweichen.

Mein Tipp: Mache dir immer eine Skizze der Pyramide aus der Angabe und beschrifte sie. Wenn du genau weißt, welche Pyramide du hast, dann vergleiche genau mit der Formel aus der Formelsammlung, ob und wie du diese Formel anpassen musst, dass sie zu deiner Aufgabe passt.

2. Die zweite Fehlerquelle klingt aufs erste Hinhören ebenfalls simpel. Dennoch fängt sie die Schüler immer wieder ein. Frage dich einfach selber, wie oft du im Eifer des Gefechts schon versucht hast, die Fläche eines Dreiecks mit der falschen Flächenformel auszurechnen.

Mein Tipp: Die Flächenformeln müssen einfach sitzen. Lerne sie so gut auswendig, dass man dich jederzeit mitten in der Nacht aufwecken kann und nach einer Formel fragen. Wenn du die Frage dann sofort beantworten kannst, dann hast du die jeweilige Formel drauf. Solltest du noch überlegen müssen, dann wiederhole die Formeln zum Berechnen der verschiedensten Flächeninhalte einfach auf LEARNZEPT.de.
Helfen bei der Auswahl der richtigen Formel kann dir wie immer eine Skizze!

3. Die dritte Fehlerquelle ist der Begriff der Höhe. Bei Pyramiden musst du immer genau schauen, welche Höhe in deiner Figur angegeben ist. Nicht selten ist es nämlich die Körperhöhe. Diese bringt dir bei der Oberflächenberechnung leider gar nichts. Über den Satz des Pythagoras kannst du die Seitenhöhe, die du brauchst aber berechnen. Siehe oben. Da hab ich dir das Problem schon erläutert.

Mein Tipp: An dieser Stelle kommt von mir immer wieder der Ratschlag: Mache dir eine beschriftete Skizze! Die hilft dir, weil du einfach vor Augen hast, welche Höhe gegeben ist und ob du sie erst berechnen musst, bevor du mit der Flächenberechnung beginnen kannst.

4. Der vierte Fehler ist ein Lieblingsfehler der Schüler, der sich durch das gesamte Stoffgebiet der Geometrie zieht, nämlich die Maßeinheiten. Sie müssen IMMER einheitlich verwendet werden, um nicht die sprichwörtlichen Äpfel mit Birnen zu vergleichen. Übrigens wird die Fläche in Quadratmetern oder Quadratzentimetern usw. angegeben.

Mein Tipp: Wenn du deine Skizze beschriftest, dann mach dies gleich mit einer einheitlichen Maßeinheit. Gib alle Maße entweder in Metern, Zentimetern oder Millimetern an. Wenn du dafür ein paar Maße umrechnen musst, ist es die Arbeit wert, weil du dadurch tatsächlich Fehler vermeiden kannst!

Oberflächeninhalt Pyramide: 6 Schritte zur perfekten Reihenfolge zur Oberflächenberechnung

Skizze anfertigen!
Skizze mit einheitlichen Maßeinheiten beschriften!
Skizze genau ansehen! Welche Flächen hast du? Welche Werte zur Berechnung hast du gegeben, welche musst du berechnen? Musst du eine Höhe mit dem Satz des Pythagoras berechnen?
Formeln aufschreiben, bevor du mit der eigentlichen Rechnung beginnst!
Stück für Stück die Oberfläche berechnen und nicht zu viele Rechenschritte auf einmal machen!
Überprüfe dein Ergebnis genau auf die richtigen Maßeinheiten! („hoch 2“ bei Flächen!)

Oberflächeninhalt Pyramide: Hier bekommst du Hilfestellung

Benötigst du weiterführende, übersichtliche Erklärungen zum Thema Oberflächeninhalt Pyramide? Bist du auf der Suche nach weiterem Übungsmaterial?

Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.

(4 Bewertung/en, durchschnittlich: 4,50 von 5)