Mitternachtsformel: Richtig rechen mit 5 Tipps

Warum nur hat man einer Formel einen so schönen und klangvollen Namen gegeben? Damit die Schüler sich das wichtigste Werkzeug auch merken können, das sie zur Lösung quadratischer Gleichungen, in denen gleichzeitig ein x² und ein x vorkommen, anwenden müssen. Und ganz erfolglos war die Benennung nun nicht, da der Begriff „Mitternachtsformel“ meiner Unterrichtserfahrung nach praktisch allen Schülern bekannt ist. Und das ist auch gut so! Diese Formel ist wichtig! Nicht alles im Mathematikunterricht ist gleich wichtig, aber die Mitternachtsformel ist es! Sie ist übrigens auch nicht besonders schwer. Ich werde dir im folgenden Text die Anwendung der Mitternachtsformel so einfach und übersichtlich wie möglich erklären. Du brauchst sie dann bloß noch üben, aber das ist dann deine Aufgabe. Es wird wichtig! Packen wir’s an!

Warum eigentlich Mitternachtsformel? Weil man dich mitten in der Nacht aufwecken und nach der Formel fragen kann, die du dann wie aus der Pistole geschossen herunterrattern können musst. Schreiben wir uns die Formel einmal auf:

Hui! Sieht ja interessant aus! Eine bunte Ansammlung von Zahlen, Buchstaben und Rechenzeichen! Jetzt aber bloß keine Angst kriegen. Ich werde dir im folgenden Text alle Bestandteile der Mitternachtsformel so unkompliziert wie möglich erklären. Das schaffen wir schon. Schau dir erstmal das folgende Video zum Thema an und wenn du dann noch Fragen hast, dann lies  einfach weiter im Text.

 

Mitternachtsformel: Erklärvideo

Was genau berechnest du eigentlich mit der Mitternachtsformel?

Wie bereits oben erwähnt, benötigst du die Mitternachtsformel zur Lösung quadratischer Gleichungen, in denen gleichzeitig ein x² und ein x vorkommen. Um die Mitternachtsformel anwenden zu können muss diese Gleichung in einer bestimmten Form geschrieben werden, nämlich:

ax² + bx + c = 0

(Die Vorzeichen in dieser Ausgangsgleichung spielen keine Rolle. Wenn wir gleich genauer besprechen, wie man mit der Mitternachtsformel rechnet, dann gehen wir darauf aber nochmal genauer ein. Zunächst kannst du dir merken, dass alle beiden Pluszeichen genauso auch Minuszeichen sein könnten. Sie können auch unterschiedlich sein.)

Ein konkretes Beispiel wäre:

-0,25x² – 0,5x + 2 = 0

Dadurch, dass die Gleichung gleich NULL gesetzt wird, erkennst du auch, dass du damit die Nullstellen einer quadratischen Funktion mit der gegebenen Funktionsgleichung bestimmst, wenn du diese Gleichung löst. Die Werte, die du für x als Lösung erhältst bedeuten ja, dass die Gleichung gleich NULL wird, wenn du diese x-Werte einsetzt. Damit weißt du an welchen Stellen der Graph der Funktion die x-Achse schneidet. Und damit hast du eben dann die Nullstellen.

Kurz gesagt:

1. Die Mitternachtsformel liefert dir die Lösung (oder auch mehrere Lösungen) einer quadratischen Gleichung.
2. Da die Gleichung zur Anwendung der Mitternachtsformel gleich NULL gesetzt wird, erhältst du gleichzeitig die Nullstellen der Gleichung.

Wie genau wendest du die Mitternachtsformel denn nun an?

Lass uns hier vorweg erstmal einen leider notwendigen Fachbegriff klären, nämlich den der „Diskriminante“. Kannst du dich noch erinnern, wie die Formel ausgesehen hat? Hier ist sie noch einmal:

Du siehst unter dem Wurzelzeichen ein großes D. Dieses D steht für Diskriminante. Mit D kannst du aber nicht rechnen. Und was jetzt? Kannst du dich noch an den allgemeinen Ansatz einer quadratischen Gleichung erinnern? Hier ist auch er noch einmal:

ax² + bx + c = 0

Die Diskriminante hat nun die folgende Formel:

D = b²  –  4 ∙ a ∙ c

Die Diskriminante besteht also aus der Zahl vor dem x zum Quadrat MINUS viermal dem Wert vor dem x² mal dem Wert für c. Naja, das musst du dir halt einfach merken. Die Mitternachtsformel und die Formel für die Diskriminante stehen aber auch in der Formelsammlung. Wobei, sicherer ist es natürlich, wenn du sie auswendig weißt.

Wenn du die Diskriminante berechnet hat, dann setzt du sie gemeinsam mit den anderen Werten in der Mitternachtsformel ein und löst die Gleichung auf. Wie das funktioniert sehen wir uns wohl jetzt mal am konkreten Beispiel an.

 

Mitternachtsformel: Ein Musterbeispiel!

Nehmen wir das Musterbeispiel von oben:

-0,25x² – 0,5x + 2 = 0

Folgende Werte haben wir (Achtung! Vorzeichen beachten!):

a = -0,25     /     b = -0,5     /     c = 2

Die Diskriminante lautet also laut Formel:

D  =  (-0,5)² – 4 ∙ (-0,25) ∙ 2  =  2,25

Wir setzen also für das große D den Wert 2,25 in die Mitternachtsformel ein. Diese sieht dann folgendermaßen aus:

Jetzt könnten wir diese Formel eigentlich bequem ausrechnen. Schließlich kommen nur noch Zahlen vor und die kann man einfach in der Taschenrechner eingeben. Da aber im Zähler zwei unterschiedliche Vorzeichen vor der Wurzel stehen, müssen wir zweimal rechnen, nämlich einmal mit dem PLUS und einmal mit dem MINUS. Ich habe dir das Problem noch einmal farblich veranschaulicht:

Wenn wir die Formel mit beiden Vorzeichen ausrechnen, dann kommen wir auch zu zwei unterschiedlichen Ergebnissen:

Die beiden Lösungen x₁ = -4 und x₂ = 2 sind jetzt nicht nur die zwei Lösungen der Gleichung sondern gleichzeitig die beiden Nullstellen der Funktion.

 

Die wichtigsten Fehlerquellen bei der Anwendung der Mitternachtsformel!

Die erste wichtige Fehlerquelle bei der Anwendung der Mitternachtsformel ist, dass sie eine ganz spezielle Form voraussetzt, in der die quadratische Gleichung stehen muss. Schüler erkennen oft nicht, dass sie die Mitternachtsformel anwenden müssen, weil rechts und links des Gleichheitszeichens unterschiedliche Faktoren und Ausdrücke stehen. Sehr oft werden dann Wurzeln gezogen an Stellen wo es nicht erlaubt ist. Ein sinvolles Ergebnis lässt sich dann natürlich nicht berechnen.

Mein Tipp: Genau hinsehen, ob du eine Gleichung hast, in der ein x² und ein x vorkommen. Wenn das zutrifft, dann vereinfache die Gleichung so, dass rechts vom Gleichheitszeichen NULL steht und der Rest aussieht wie in der allgemeinen Form, die wir oben bereits gesehen haben. Hier ist sie nochmal zur Wiederholung:

ax² + bx + c = 0

 

Die zweite wichtige Fehlerquelle ist ein Rechenfehler, der Schülern nicht nur beim Auflösen der Mitternachtsformel Probleme macht. Bei der Berechnung der Diskriminante kann es passieren, dass man für den Ausdruck b² eine negative Zahl quadrieren muss. Hier musst du darauf aufpassen, dass du auf jeden Fall eine Klammer um die negative Zahl setzt. Eine negative Zahl wird nämlich beim Quadrieren bekanntlich positiv und somit fällt das Minuszeichen weg. Setzt du die Klammer nicht, dann bleibt das MINUS stehen und das ist falsch.

Mein Tipp: Bei negativen Zahlen besonders aufmerksam die Diskriminante berechnen und die Klammer immer setzen!

 

Die dritte wichtige Fehlerquelle besteht darin, dass Schüler oft nicht beachten, dass wenn vor dem x² oder dem x kein Koeffizient (keine Zahl) steht, mit dem Wert 1 gerechnet werden muss. Schüler denken dann oft: „Wenn nichts davor steht, dann rechne ich mit NULL, weil nichts bedeutet ja NULL.“ Das ist falsch und du bekommst beim Lösen der Mitternachtsformel dann einen vollständig anderen und falschen Wert heraus.

Mein Tipp: Merk dir einfach, dass du mit dem Wert 1 rechnen musst, wenn vor einer Variable keine andere Zahl steht!

 

Mitternachtsformel: Mit 5 Tipps geht nichts mehr schief!

1. Stelle eine quadratische Gleichung, in der x²  und x vorkommen immer so um, dass auf der rechten Seite NULL steht und die Gleichung aussieht wie die allgemeine Form:    ax² + bx + c = 0
2. Schreibe dir die Werte für a, b und c extra auf und beachte das Vorzeichen. Denke dir eine 1 wenn es einen der drei Werte in deiner Gleichung nicht gibt.
3. Berechne die Diskriminante und setze sie in die Mitternachtsformel ein.
4. Berechne die Lösung für beide Vorzeichen vor der Wurzel. Bedenke, du solltest zwei Lösungen herausbekommen.
   (Nur in Spezialfällen hast du nur eine oder keine Lösung. Erklärvideos und Übungsaufgaben hierzu findest du auf der Seite LEARNZEPT.de.)
5. Überprüfe dein Ergebnis und schreibe die Lösungsmenge und, wenn es gefragt ist, die Nulllstellen in Koordinatenschreibweise auf.

 

Mitternachtsformel: Hier bekommst du Hilfestellung

Wie wäre es, wenn du die Anwendung der Mitternachtsformel und ihre Fallstricke übersichtlich und leicht verständlich wiederholen könntest? Möchtest du mit echten Klassenarbeiten und ausführlichen Erklärungen und Lösungen auf die nächste Prüfung lernen?

Erklärvideos und echte, interaktiv aufbereitete Klassenarbeiten zur Übung gibt’s nur auf der Online-Lernplattform Learnzept! Klicke hier für einen kostenlosen Account!

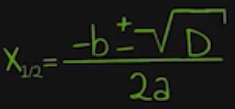
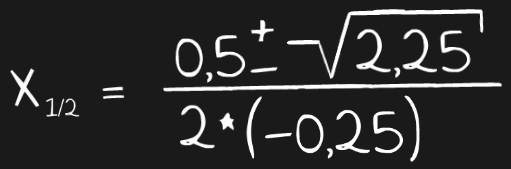
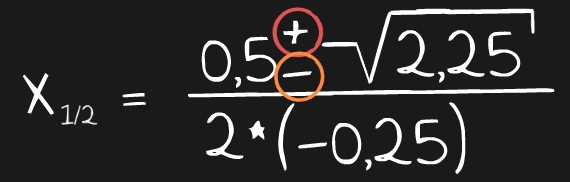
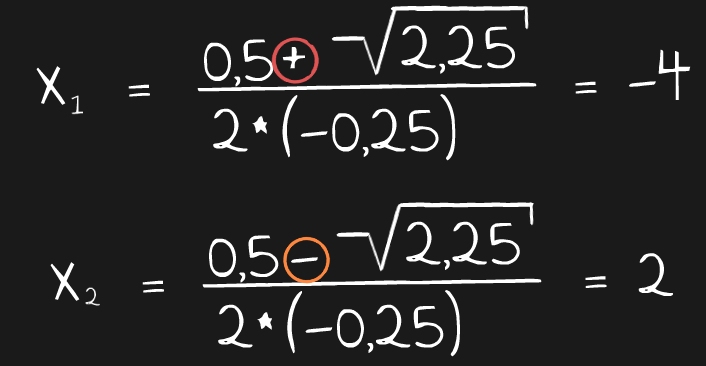
(4 Bewertung/en, durchschnittlich: 3,25 von 5)

Loading...