Polynomdivision: 4 Tipps für’s richtige Ergebnis

 

Die Polynomdivision ist weniger ein tatsächliches mathematisches Thema als ein Werkzeug für ein mathematisches Thema. Du brauchst die oft zur Bestimmung der Nullstellen bei Funktionen 3. Grades. Eine Funktion 3. Grades hast du dann, wenn in der Funktionsgleichung ein x³ vorkommt. Der Begriff Polynomdivision kling jetzt natürlich furchtbar kompliziert, aber ich werde versuchen, dir ohne allzu viele lästigen Fachbegriffe und direkt zum Punkt das Wichtigste zur Polynomdivision zu erklären, so dass du in Klassenarbeiten keine Schwierigkeiten mehr damit hast.

Wie du die Nullstellen bei einer Funktion 3. Grades bestimmst, gehen wir knapp an einem Beispiel durch:

f(x) = x³ – 2x² – 11x + 12

Die erste Nullstelle findest du durch Ausprobieren heraus. Da wir hier im Text möglichst schnell zur Polynomdivision kommen wollen, verweise ich dir für Fragen, wie du am besten „ausprobierst“ am besten auf die Seite LEARNZEPT.de.

Du wirst beim Ausprobieren jedenfalls auf eine Nullstelle bei x₁ = 4 kommen.

Die zweite Nullstelle findest du jetzt durch Polynomdivision.

Schau dir zunächst das folgende Erklärvideo an. Darin wird dir die Technik der Polynomdivision ausführlich erklärt. Solltest du danach noch Fragen zur Polynomdivision haben, dann lies einfach im Text weiter. Ich werde dich im weiteren Verlauf auch auf die wichtigsten Fehlerquellen hinweisen, die in Klassenarbeiten sehr oft versteckt sind.

 

Polynomdivision: Erklärvideo

Im Video wird dir erklärt, wie du mithilfe der Polynomdivision bequem Nullstellen einer Funktion ausrechnen kannst.

Polynomdivision: Wie mache ich das und worauf muss ich achten?

Zwei Dinge haben wir gegeben und oben bereits erwähnt.

1. Folgende Funktionsgleichung: f(x) = x³ – 2x² – 11x + 12
2. Bereits eine Nullstelle durch Probieren: x₁ = 4

Um weitere Nullstellen der Funktion herauszufinden musst du jetzt eine Polynomdivision durchführen. Diese sieht zunächst folgendermaßen aus:

x³ – 2x² – 11x + 12 : (x – 4)

Du teilst also deine Funktionsgleichung durch einen Term „x – erste Nullstelle“

Achtung!
Das „Minus“ entsteht, weil die erste Nullstelle 4 ist und du das Vorzeichen für die Polynomdivision laut Regel immer umdrehen musst!
Wäre die Nullstelle -4 gewesen, dann hättest du durch (x + 4) teilen müssen.

Hoffentlich kannst du nachvollziehen, was ich damit meine, aber einfacher kann man es nicht wirklich ausdrücken. Im folgenden Bild hab ich dir die Polynomdivision oben mal ausgerechnet. Sieh dir die Grafik zuerst mal an und dann schreibe ich noch ein paar Zeilen dazu.

Fassen wir mal in Worten zusammen:

Als erstes dividierst du die größte Potenz, also x³ durch x. Dadurch erhältst du hinter dem Gleichheitszeichen das x². Wenn du jetzt im Gegenzug mit dem x²  den Term (x – 4) wieder malnimmst, dann kommst du auf (x³ – 4x²). Dieses Ergebnis schreibst du dann unter den Ausgangsterm und, wie du es beim „Schriftlich Teilen“ in der Unterstufe gelernt hast, ziehst die beiden Terme voneinander ab.

Dabei musst du auf die Vorzeichen achten, weil du, wie du siehst vor den Klammern ein „Minus“ hast, das dir jedesmal die Vorzeichen in der Klammer ändert. Hierzu mehr gleich.

Den oben beschriebenen Schritt wiederholst du so oft, bis du unten bei der „Null“ angekommen bist.

Wenn du am Ende der Polynomdivision eine „Null“ als Ergebnis herausbekommst, dann bist du erstmal fertig. Deinen Ergebnis-Term…

…kannst du jetzt in die sogenannte Mitternachtsformel einsetzen und so die Nullstellen ermitteln. Die Anwendung der Mitternachtsformel wird dir ausführlich und übersichtlich auf der Seite LEARNZEPT.de erklärt.

 

Polynomdivision: Die Vorzeichen als Fehlerquelle

Die Polynomdivision ist eigentlich nur eine einfache Rechenoperation, die du sauber und Schritt für Schritt durchziehen musst. Die Betonung liegt dabei allerdigs auf dem „eigentlich“. Die Polynomdivision ist in der Theorie auch einfach, allerdings fallen Schüler sehr oft in die Vorzeichenfalle.

Wie oben in der Grafik gesehen und auch erklärt muss immer ein Term von einem anderen abgezogen werden. Dabei steht dann immer ein „minus“ vor der Klammer. Einen Ausschnitt der Rechnung von oben hab ich zur Erklärung mal abgebildet, damit du auch sehen kannst, wovon ich rede.

Beim ersten Teil (2x² – 2x²) gibt’s normalerweise noch keine Probleme. Dabei kommt „Null“ heraus und wir können die Stelle dann im Ergebnis weglassen. Beim zweiten Teil wird’s knifflig. Du musst nämlich, weil das „Minus“ vor der Klammer das Vorzeichen in der Klammer ändert folgendermaßen rechnen:

-11x + 8x

Dabei erhältst du dann wie du siehst -3x als Ergebnis. Dieser Fehler passiert sehr oft in Klassenarbeiten. Deswegen habe ich ihn als einzigen großen Fehler bei der Polynomdivision besonders betont und auch einen Tipp für dich. Nimm einen Farbstift zur Hand und ersetze das Vorzeichen in der Klammer einfach durch sein Gegenteil und du machst den Fehler nicht mehr.

Schau dir die Grafik an. So ist das gemeint:

Jetzt darfst du dir nur nicht zu schade sein, den Trick auch anzuwenden. Ich habe ihn im Lauf der Jahre hunderten Schülern so gezeigt und sie fanden ihn klasse. In der Klassenarbeit waren sie sich für so einen „Kleinkindertrick“ dann aber zu schade und haben dafür lieber den Fehler gemacht und die schlechte Note kassiert. Finde ich persönlich nicht besonders clever. Du etwa?

 

Polynomdivision: Mit 4 Tipps zum richtigen Ergebnis

Die folgenden Tipps solltest du bei der Polynomdivision für jede Zeile anwenden, dann kommst du ziemlich sicher zum richtigen Ergebnis:

1. Schreibe die Rechnung sauber auf.
   Bedenke, du musst immer mit dem umgekehrten Vorzeichen rechnen: „Minus“, wenn deine erste Nullstelle positiv ist und „plus“ wenn deine erste Nullstelle negativ ist.
2. Teile Zeile für Zeile und pass auf, dass du dich nicht verrechnest!
3. Schreibe dir IMMER bunt das richtige Vorzeichen in die Klammer, wie ich es dir oben erklärt habe.
4. Überprüfe, ob dein Ergebnis stimmt.
   Keine Sorge, wenn ein Rest bei der Polynomdivision herauskommt. Das ist durchaus möglich. Mit dem Rest lassen sich in der Kurvendiskussion noch allerhand lustige Sachen bereechnen. Was genau und wie du damit umgehst, kannst du dir auf der Seite LEARNZEPT.de genau erklären lassen.

 

Polynomdivision: Hier bekommst du Hilfestellung

Wie wäre es, wenn du die Polynomdivision und ihre Vorzeichen-Fallstricke übersichtlich und leicht verständlich wiederholen könntest? Möchtest du mit echten Klassenarbeiten und ausführlichen Erklärungen und Lösungen auf die nächste Prüfung lernen?

Erklärvideos und echte, interaktiv aufbereitete Klassenarbeiten zur Übung gibt’s nur auf der Online-Lernplattform Learnzept! Klicke hier für einen kostenlosen Account!

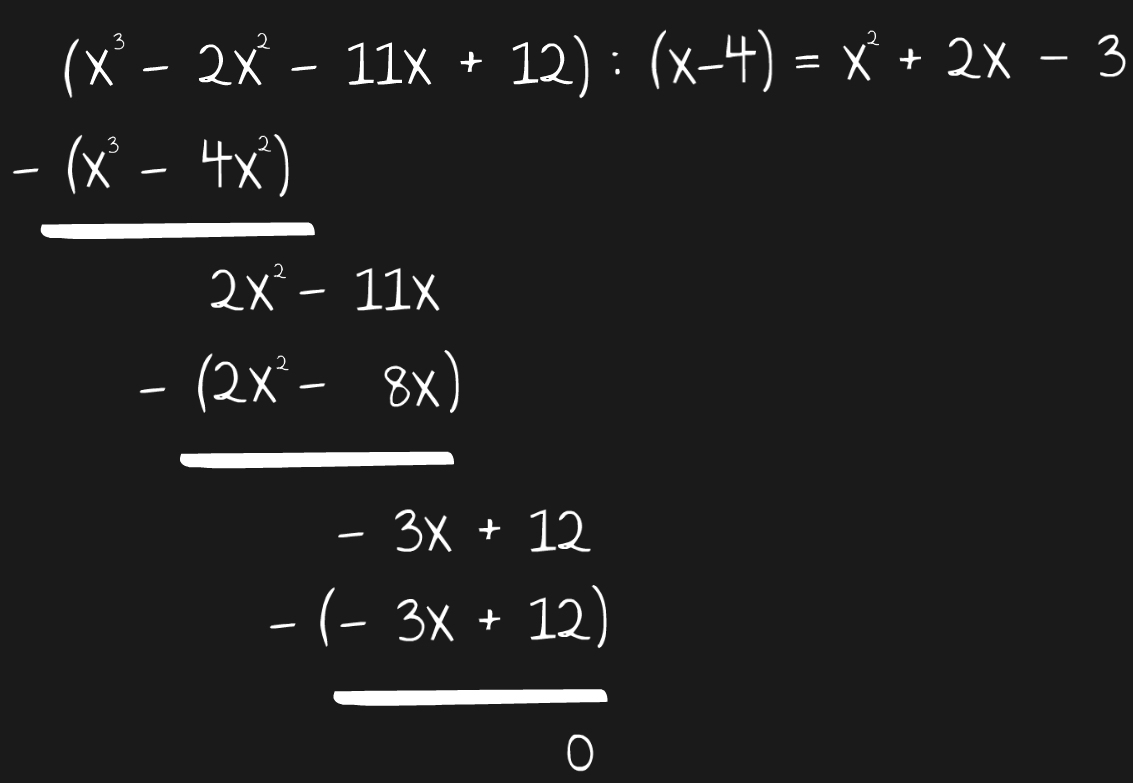
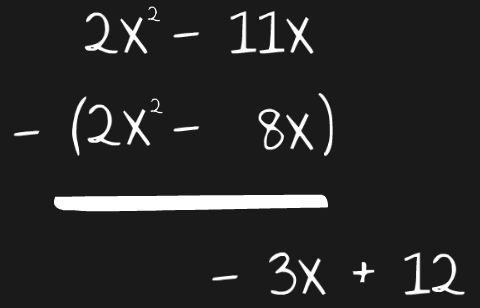
(2 Bewertung/en, durchschnittlich: 4,00 von 5)

Loading...