Potenzen mit rationalen Exponenten: 3 hilfreiche Tipps

In diesem Text klären wir die Bedeutung von Potenzen mit rationalem Exponenten und wie du damit rechnen kannst. Hier lernst du, was ein rationaler Exponent ist und welche Bedeutung er für die Potenz hat. Ich zeige dir, welcher Zusammenhang zwischen einer Potenz mit rationalem Exponenten und einer sogenannten „n-ten Wurzel“ besteht und wie du sie ineinander umrechnen kannst. Wir fangen einfach an. Du wirst sehen, dass auch rationale Exponenten gar nicht so schwer sind.

Exponenten sind Hochzahlen, also zum Beispiel die 3 beim Ausdruck x³.

Rationale Exponenten sind also Exponenten aus der Menge der Rationalen Zahlen „Q“ .

Die Hochzahlen sind also Brüche. ¼ ist demnach der rationale Exponent bei x^1/4.

Potenzen mit rationalen Exponenten: Erklärvideo

Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren

Video laden

YouTube immer entsperren

Potenzen mit rationalen Exponenten: Was solltest du zu diesem Thema wissen?

Wir beschäftigen uns beim Thema Potenzen mit rationalen Exponenten mit Ausdrücken wie x^1/2.

Aber was ist das dann?

Folgende Aussagen können wir aufgrund der Potenzregeln treffen:

Darum muss x^1/2 = $\sqrt{x}$ sein, denn nur $\sqrt{x} \quad \cdot \quad \sqrt{x} \quad = \quad x$

Ganz allgemein gilt:

Der Nenner gibt also an, um die „wievielte Wurzel“ es sich handelt. Der Zähler bleibt als Potenz erhalten.

Eine besondere Bedeutung hat dabei der Ausdruck x^1/n. Denn x^1/n ist gerade die „n-te Wurzel“ aus x.

Mathematisch ausgedrückt gilt: x^1/n = $\sqrt[n]{x}$

Und was bringt dir das jetzt?

Du kannst alle Rechenregeln für Potenzen auch auf Wurzeln anwenden. Dazu gehören natürlich die Potenzregeln, aber später zum Beispiel auch manche Ableitungsregel.

Ausführliche Erklärungen zu den Ableitungsregeln bietet dir die Seite LEARNZEPT.de.

Es gibt kaum etwas Ärgerlicheres, als eine komplizierte Regel zu können und dann wegen so etwas Einfachem wie der Umformung von Wurzeln in Potenzen in einer Aufgabe nicht weiterzukommen. Darum empfehle ich dir, das Umformen von Wurzeln in Potenzen gut zu üben. Dies kannst du auch ausführlich anhand vieler interaktiver Übungsaufgaben auf der Seite LEARNZEPT.de tun. Du wirst es später immer wieder brauchen.

Die Potenzen mit rationalem Exponenten sind also nur eine andere Schreibweise für Wurzelausdrücke. Das kann gerade an Computern oft hilfreich sein, da ein Wurzelzeichen nicht immer zu finden ist.

Auch Vereinfachungen sind oft in der Potenzschreibweise leichter zu entdecken.

Beispiele:

Potenzen mit rationalen Exponenten: Fehlerquellen in Aufgaben

Es passiert leider leicht, den Nenner und den Zähler zu verwechseln. Der Exponent geht immer in den Zähler, die Zahl bei der Wurzel immer in den Nenner.
Sehr wichtig ist es auch, zu wissen, dass sich eine Wurzel als Potenz schreiben lässt. Viele Schüler vergessen das und kommen dann oft in Klassenarbeiten nicht weiter, da ihnen das entsprechende Wurzelgesetz fehlt.

Potenzen mit rationalen Exponenten: 3 hilfreiche Tipps

$\sqrt{x}$ = x^1/2
Alle Wurzeln lassen sich auch als Potenz schreiben.
Durch das Umschreiben von Potenzen in Wurzeln und anders herum ist es oft einfacher zu erkennen, was sich kürzen lässt.

Potenzen mit rationalen Exponenten: Hier bekommst du Hilfestellung

Benötigst du weiterführende, übersichtliche Erklärungen zum Thema Potenzen mit rationalen Exponenten? Bist du auf der Suche nach weiterem Übungsmaterial?

Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.

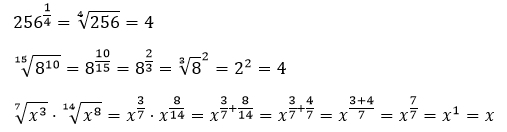
(8 Bewertung/en, durchschnittlich: 3,88 von 5)