Oberflächeninhalt Zylinder: 4 Tipps zur Flächenberechnung

Das Thema Oberflächeninhalt Zylinder wird von Lehrern oft recht umständlich erklärt. Eigentlich kann man das Volumen eines Zylinders aber recht leicht verstehen, wenn man es mit ein wenig Struktur behandelt. Eines vorweg: Fehleranfällig ist das Thema Oberflächeninhalt Zylinder manchmal deshalb, weil die Grundfläche eines Zylinders ein Kreis ist und man da zwischen Umfang und Fläche unterscheiden muss. Aber auch dies ist überschaubar und erstmal eines nach dem anderen.
Beantworten wir zunächst einmal die Frage, was ein Zylinder ist und aus welchen ein Zylinder besteht.
Ein Zylinder sieht aus wie ein rundes Rohr oder wie eine Getränkedose.
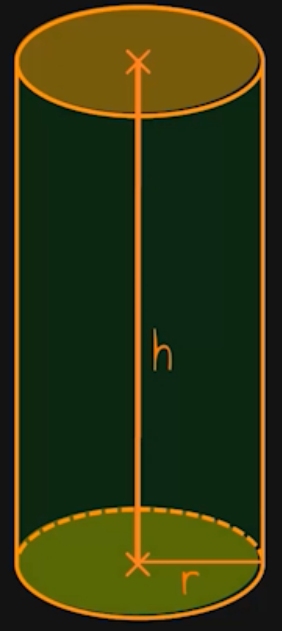
Ein Zylinder ist in gerader Körper. Gerader Körper bedeutet, dass er eine Grundfläche und eine Deckfläche hat, die parallel und deckungsgleich sind. Beim Zylinder sind beides natürlich Kreisflächen. Die Entfernung zwischen den beiden Kreisflächen ist die Zylinderhöhe. Neben den beiden Kreisflächen oben und unten besitzt ein Zylinder noch eine Mantelfläche. Die Oberfläche besteht dann eben aus den beiden Kreisflächen und der Mantelfläche.
Soviel vorweg. Sieh dir zunächst mal das folgende Video an. Du bekommst in dem Video einen Überblick über die Flächenberechnung beim Zylinder und die Formeln, die du dabei benötigst.
Wenn du danach noch Fragen zum Thema Oberflächeninhalt Zylinder hast und wenn du besonders daran interessiert bist, welche speziellen Fehler Schüler beim Berechnen häufig machen und wie du diese vermeiden kannst, dann lies im Text einfach weiter.
Oberflächeninhalt Zylinder: Erklärvideo
Im Video wird dir erklärt, wie du mithilfe von Kreisumfang und -fläche bequem die Oberfläche eines Zylinders ausrechnen kannst.
Oberflächeninhalt Zylinder: Welche Kenntnisse musst du für Klassenarbeiten haben?
Wiederholen wir noch einmal das Offensichtliche: Ein Zylinder ist ein Körper mit einer Grundfläche, einer Deckfläche und einer Mantelfläche. Grund- und Deckfläche sind zwei parallele und gleich große Kreise.
Wenn du die Oberfläche berechnen willst musst du einfach die Grundfläche, die Deckfläche und die Mantelfläche zuammenzählen. Da Grund- und Deckfläche identisch sind kommen wir mathematische zur folgenden Formel:
(in Worten: Oberfläche = 2 • Grundfläche + Mantelfläche)
Da wir außerdem wissen, dass die Grundfläche ein Kreis ist wissen wir auch die Flächenformel für die Grundfläche:
Wenn du die geometrischen Berechnungen am Kreis nochmal wiederholen und üben möchtest, dann findest du Erklärungen und Übungsmaterial auf der Seite LEARNZEPT.de.
Du kannst unsere Formel für die Oberfläche also auch so schreiben, dass die Formel für die Grundfläche bereits integriert ist:
Die Mantelfläche berechnet sich folgendermaßen:
(in Worten: Mantelfläche = 2 • Kreisumfang • π • Höhe des Zylinders)
Auch die Formel für die Mantelfläche kannst du in die Oberflächenformel integrieren. Mit ein wenig Umstellarbeit kommst du dann zu folgender Formel für die Oberfläche, die du auswendig lernen kannst:
Ich habe dir hier die Formel in der Endform aufgeschrieben. Wenn du wissen möchtest, wie du das Umstellen von Formeln selbständig auf alle anderen Formeln anwenden möchtest, dann kannst du dies auf der Seite LEARNZEPT.de üben.
Das war’s eigentlich, was zur Berechnung der Oberfläche einer Pyramide zu sagen ist. Sehen wir uns im Folgenden ein paar typisch Fehler an, die Schülern immer wieder unterlaufen.
Oberflächeninhalt Zylinder: Welche typischen Schüler-Fehler musst du vermeiden?
1. Der erste Fehler, den Schüler nach meiner Unterrichtserfahrung gerne machen, liegt daran, dass sie beim Kreis die Formeln für Umfang und Fläche verwechseln. zur Berechnung der Oberfläche brauchst du nämlich beide Formeln. Wenn du die Oberfläche berechnen willst, dann brauchst du die Grundfläche und die Deckfläche. Diese beiden berechnest du mit der Flächenformel des Kreises:
A = r2 • π
Außerdem brauchst du für die Oberfläche die Mantelfläche des Zylinders. Die Mantelfläche jedoch berechnest du nicht mit der Flächenformel des Kreises, sondern mit seinem Umfang, nämlich Umfang • Höhe des Zylinders:
Mein Tipp: Du kannst bei der Oberflächenberechnung auf zwei Weisen vorgehen. Entweder du merkst dir die Oberflächenformel, die wir oben bereits angegeben haben. Du kannst aber auch zuerst die beiden Kreisflächen und dann die Mantelflächen berechnen und dann alle drei Flächen zusammenzählen. dann muss du dir merken:
Grundflächen: „Ich brauche die Flächenformel beim Kreis!“
Mantelflächen: „Ich brauche die Formel für den Kreisumfang!“
Weitere Erklärungen zur Berechnung von Kreisumfang und Kreisfläche findest du auf der Seite LEARNZEPT.de.
2. Der zweite Fehler ist ein Lieblingsfehler der Schüler. Er wird im gesamten Fachgebiet der Geometrie gerne gemacht. Maßeinheiten müssen IMMER einheitlich verwendet werden, ansonsten kann es gut passieren, dass du Äpfel mit Birnen vergleichst. Übrigens wird die Fläche in Quadratmetern oder Quadratzentimetern usw. angegeben. Das heißt: „Hoch 2“ beim Ergebnis nicht vergessen!
Mein Tipp: Eine Skizze hilft immer. Beschrifte diese dann immer gleich mit einer einheitlichen Maßeinheit. Gib alle Maße entweder in Metern, Zentimetern oder Millimetern an. Solltest du dafür ein paar Maße umrechnen müssen, dann mach dir diese Arbeit trotzdem. Du kannst dadurch tatsächlich Fehler vermeiden!
Oberflächeninhalt Zylinder: 4 Schritte und die Rechnung stimmt!
- Fertige eine Skizze an!
- Beschrifte deine Skizze mit einheitlichen Maßeinheiten! Die Arbeit, ein paar Maßeinheiten umzurechen lohnt sich!
- Entscheide dich für eine Vorgehensweise: Entweder die umfassende Gesamtformel für die Oberfläche…
…oder die Einzelflächen:Grundflächen: „Ich brauche die Flächenformel beim Kreis!“Mantelflächen: „Ich brauche die Formel für den Kreisumfang!“
- Überprüfe dein Ergebnis nochmal, ob du mit gleichen Maßeinheiten gerechnet hast und ob du das Ergebnis in der richtigen Benennung (m2, cm2, mm2, usw.) angegeben hast. Flächen geben wir mit „hoch 2“ an!
Oberflächeninhalt Zylinder: Hier bekommst du Hilfestellung
Wie wäre es, wenn du das Thema Oberflächeninhalt Zylinder übersichtlich und leicht verständlich wiederholen könntest?
Möchtest du mit echten Klassenarbeiten und ausführlichen Erklärungen und Lösungen auf die nächste Prüfung lernen?
Erklärvideos und echte, interaktiv aufbereitete Klassenarbeiten zur Übung gibt’s nur auf der Online-Lernplattform Learnzept! Klicke hier für einen kostenlosen Account!





Entschuldigung, Kommentare zu diesem Artikel sind nicht möglich.