Thalessatz: 2 wichtige Tipps im rechtwinkligen Dreieck

Der Thalessatz ist einer der bekanntesten Sätze aus der Mathematik. In diesem Text zeige ich dir, welche Aussagen der Thalessatz trifft und wie er dir beim Konstruieren von rechtwinkligen Dreiecken und Tangenten helfen kann.

Der Thalessatz lautet folgendermaßen:

„Ein Dreieck ist genau dann rechtwinklig im Punkt C, wenn sich C auf dem Halbkreis über der Strecke AB befindet.“ Diesen Halbkreis bezeichnet man als Thaleskreis.

Beachte beim Thalessatz das „genau dann“. Es verrät dir, dass der Thalessatz in beide Richtungen funktioniert. Das ist nicht selbstverständlich, aber für dich sehr nützlich.

Aber jetzt erstmal genug der verwirrenden Worte. Schau dir erstmal das folgende Video an. Es erklärt dir ausführlich, was es mit dem Thalessatz auf sich hat und wie er dir beim Konstruieren von Dreiecken und Tangenten hilft. Wenn du danach noch Fragen haben solltest, dann lies einfach weiter im Text.

 

Thalessatz: Erklärvideo

In diesem Video wird dir ausführlich erklärt wie du den Thalessatz anwenden kannst.
 
 

 
 

Thalessatz: Wichtiges Grundwissen zur Konstruktion rechtwinkliger Dreiecke

 Wann hilft mir der Thalessatz?

Der Thalessatz ist ziemlich einfach. Daher empfehle ich dir, immer wenn es geht, den Thalessatz zu verwenden. Brauchst du irgendwo einen Rechten Winkel und hast die gegenüberliegende Strecke gegeben, zeichne einen Thaleskreis. Meistens geht es zwar auch irgendwie anders, aber der Thaleskreis ist fast immer einfacher.

 

Beispiele

Beispiel 1:

Gegeben:                                   c = 12cm   /   γ = 90°   /   α = 40°

Gesucht:                                     Dreieck ABC

Konstruktionsplan:
Halbiere die Strecke AB und ziehe einen Thaleskreis k um diesen Mittelpunkt M durch A (und damit auch durch B). Auf k muss C liegen. Jetzt trägst du den Winkel an und am Schnittpunkt mit den Kreis liegt C.

 

Beispiel 2:

Gegeben:                                   c = 12cm   /   γ = 90°   /   b = 6cm

Gesucht:                                     Dreieck ABC

Konstruktionsplan:
Halbiere die Strecke AB und ziehe einen Thaleskreis k um diesen Mittelpunkt M durch A. Ziehe einen weiteren Kreis um A mit Radius 6cm. Am Schnittpunkt liegt wieder C.

 

Beispiel 3:

Gegeben:                                   c = 12cm   /   γ = 90°   /   C ist gleich weit entfernt von A und B

Gesucht:                                     Dreieck ABC

Konstruktionsplan:
Halbiere die Strecke AB und ziehe einen Thaleskreis k um diesen Mittelpunkt M durch A. Da C von A und B gleich weit weg ist, muss C auch auf der Mittelsenkrechten von A und B liegen. Konstruiere daher die Mittelsenkrechte m. Auf dem Schnittpunkt der Mittelsenkrechte m und der Kreislinie k liegt C.

(Wie man am einfachsten eine Mittelsenkrechte konstruieren kann, kannst du dir auf der Seite LEARNZEPT.de genauer ansehen)

 

Beispiel 4:

Gegeben:                                   c = 12cm   /   γ = 90°   /   h = 3cm   /   a>b

Gesucht:                                     Dreieck ABC

Konstruktionsplan:
Halbiere die Strecke AB und ziehe einen Thaleskreis k um diesen Mittelpunkt M durch A. Konstruiere dann eine Parallele zu c mit Abstand 3 cm. Dabei erhältst du zwei Schnittpunkte, aber nur beim Linken ist a>b. Der linke Schnittpunkt ist damit C.

 

Beispiel 5:

Oft wird dir nur indirekt verraten, dass du einen rechten Winkel hast, bzw. dass es sich überhaupt um ein Dreieck handelt. Wenn z.B. eine Tangente gesucht ist, musst du erst erkennen, dass die Tangente rechtwinklig auf den Radius steht. Zusammen mit dem richtigen Dreieck kann man dann den Thaleskreis benutzen, um die Tangente zu konstruieren.

Gegeben:                                   Kreis k und ein Punkt P

Gesucht:                                    Tangente t durch den Punkt P an den Kreis k

Konstruktionsplan:
Halbiere die Strecke von P zum Kreismittelpunkt M_K und ziehe einen Thaleskreis k um diesen Mittelpunkt M durch P. Es ergeben sich zwei Kreisschnittpunkte. Beide eignen sich, um die Tangente t zu zeichnen.

 

Warum ist es jetzt wichtig, dass der Thalessatz in beide Richtungen gültig ist?

Bis jetzt hast du immer vom 90° Winkel auf den Thaleskreis geschlossen. Manchmal ist aber auch der Thaleskreis gegeben und du musst erkennen, dass Gamma dann 90° sein muss. Das klingt einfach. Aber Vorsicht, der Thaleskreis muss nicht eingezeichnet sein und ist dadurch nicht immer sofort zu erkennen.

 

Beispiel 6:

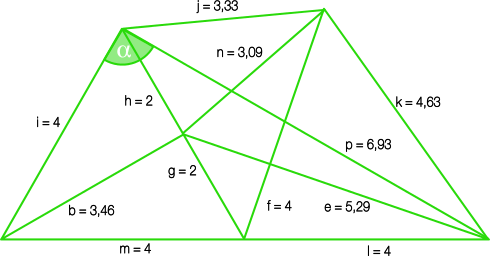
Wenn man die Längen vergleicht, kann man erkennen, dass sich ein Thaleskreis einzeichnen lässt. Damit ist sofort klar, dass Alpha 90° sein muss.

 

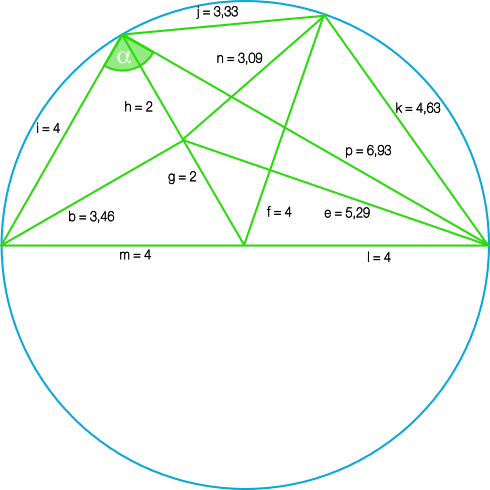
Thalessatz: Wo kannst du in der Klassenarbeit Fehler machen?

• Die größte Schwierigkeit beim Thalessatz ist, daran zu denken, dass es ihn gibt. Prüfe also immer, wenn ein rechter Winkel gegeben oder gesucht ist, ob sich der Thalessatz benutzen lässt. Denn der ist vergleichsweise einfach.
• Der Thaleskreis muss immer um den Mittelpunkt gezeichnet werden, nicht um A oder B oder C.

 

Thalessatz: Das Wichtigste in 2 Tipps

1. Sollen wir ein Dreieck mit 90° Winkel konstruieren und die gegenüberliegende Seite ist gegeben, zeichnen wir einen Thaleskreis.
2. Sollst du nachweisen, dass ein Rechter Winkel existiert, versuche ebenfalls, einen Thaleskreis zu finden.

 

Thalessatz: Hier bekommst du Hilfestellung

Benötigst du weiterführende, übersichtliche Erklärungen zum Thema Thalessatz? Bist du auf der Suche nach weiterem Übungsmaterial?

Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.

(7 Bewertung/en, durchschnittlich: 4,86 von 5)

Loading...