Volumen Prisma: 4 Schritte zur perfekten Berechnung

Was ist ein Prisma? Ein Prisma ist ein Körper aus der Raumgeometrie und zwar ein gerader Körper. Gerader Körper bedeutet, der Körper hat eine Deckfläche und eine Grundfläche. In diesem Text werde ich dir ausführlich, aber ohne unnötige Fachbegriffe erklären, wie du das Volumen eines Prismas bestimmen kannst, wie du andere Größen wie die Höhe oder die Grundfläche mit der Volumenformel berechnen kannst und welche Fehler, meiner Unterrichtserfahrung nach, den Schülern immer wieder passieren.
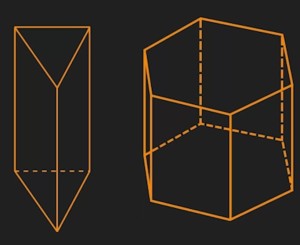
Wie bereits erwähnt, ist ein Prisma ein gerader Körper, das heißt, er läuft nicht wie zum Beispiel ein Kegel oder eine Pyramide spitz zu. Wir können also festhalten, dass ein Prisma eine Grundfläche und eine Deckfläche hat. Diese beiden Flächen sind immer parallel und deckungsgleich. Die beiden Abbildungen sind Beispiele für Prismen.
Wie du an den beiden Abbildungen erkennen kannst, können Prismen unterschiedliche Grund- und Deckflächen haben. Außerdem kannst du erkennen, dass ein Prisma neben der Grund- und der Deckfläche noch jeweils so viele Seitenflächen hat, wie die Grundfläche Ecken. So hat ein Dreiecksprisma drei Seitenflächen und ein Sechseckprisma sechs Seitenflächen. Da Prismen gerade Körper sind, können wir außerdem festhalten, dass die Höhe der Abstand zwischen der Grund- und der Deckfläche ist. Nun aber mal genug vorweg. Sieh dir erstmal das folgende Video an. Darin wird dir erklärt, wie du das Volumen eines Prismas berechnen kannst. Wenn du danach noch weiteren Erklärungsbedarf hast, lies einfach den Text weiter.
Volumen Prisma: Erklärvideo
In diesem Video erhältst du einen Eindruck davon, wie du das Volumen eines Prismas berechnen kannst.
Volumen Prisma: Welche Grundlagen benötigst du, um richtig mit Prismen rechnen zu können?
Kommen wir zuerst nochmal auf die beiden Abbildungen von oben zurück. Du kannst daran erkennen, dass ein Prisma immer ein gerader Körper ist. Gerader Körper bedeutet, der Körper hat eine Grundfläche und eine Deckfläche, die gleich groß und auch deckungsgleich sind. Man kann sie so übereinander legen, dass es so aussieht, als wäre es nur noch eine einzige Fläche.
Diese Form hat für die Berechnung des Volumens eines Prismas den Vorteil, dass man sich das Volumen so vorstellen kann, als hätte man einfach nur die Grundfläche so oft übereinander gelegt, bis die Höhe des Körpers erreicht war. Das führt uns zur folgenden Volumenformel:
Jetzt wissen wir, dass das Volumen mit der Grundfläche und der Höhe des Prismas berechnet wird. Die Grundfläche müssen wir je nach dem, ob es ein Dreieck oder ein anderes Vieleck ist, entsprechend der jeweiligen Flächenformel berechnen. Die Formeln zur Flächenberechnung der verschiedensten Flächen kannst du dir auf der Seite LEARNZEPT.de noch einmal genau ansehen.
Wenn wir die Volumenformel kennen, dann können wir diese durch Umstellung so hinschreiben, um damit auch die Grundfläche und die Höhe des Prismas berechnen zu können. Das ist in Klassenarbeiten und Schulaufgaben meiner Erfahrung nach eine häufige Aufgabenstellung.
Ich habe dir die Formel schonmal so umgestellt, dass du die Höhe und die Grundfläche berechnen kannst:
1. Grundfläche gesucht:
2. Körperhöhe gesucht:
Übungen zum Umformen der verschiedenen Formeln findest du auf der Seite LEARNZEPT.de.
Damit kennst du alle Formeln die du zum Thema Volumen Prisma benötigst. Sieht alles eigentlich ganz einfach aus, oder? Dennoch gibts die eine oder andere Fehlerquelle, auf die du in Klassenarbeiten oder Schulaufgaben vorbereitet sein solltest. Auf diese Fehlerquellen wollen wir jetzt noch genauer eingehen.
Volumen Prisma: Wo verstecken sich die Fehlerquellen?
1. Fehlerquelle Nummer eins bei Schülern ist, meiner Erfahrung nach, dass sie das Prisma nicht erkennen, wenn es vor ihnen liegt. Das Verb liegen verwende ich mit Absicht. Stell dir einen Dachboden vor. Er ist dann ein Prisma, wenn er zweimal die gleiche Wand an der einen Seite und an der anderen Seite hat. Ihn als Prisma zu erkennen ist deswegen schwer, weil er auf einer seiner Seitenflächen liegt.
Mein Tipp: Schau dir das Bild in der Angabe der Klassenarbeit oder Schulaufgabe genau an und suche zwei gleiche Flächen. Suche dann den Abstand dieser beiden Flächen zueinander und schon hast du dein Prisma gefunden!
2. Fehlerquelle Nummer zwei ist, dass du die Grundfläche erkennst. ein Prisma kann als Grundfläche ein Dreieck, aber auch ein anderes Vieleck haben. Diese Fläche musst du dann mit der jeweiligen Flächenformel berechnen. Abwechslungsreiche Erklärungen zur Berechnung der verschiedensten Flächen findest du auf der Seite LEARNZEPT.de.
Mein Tipp: Auch hier kann ich dir nur empfehlen lieber zweimal genau hinzusehen als einmal. Augen auf und richtige Formel anwenden!
3. Fehlerquelle Nummer drei bezieht sich auf die richtige Umstellung der Volumenformel. Die Volumenformel des Prismas sowie die Umstellungen zur Berechnung der Körperhöhe und Grundfläche haben wir oben ja bereits aufgeschrieben.
Mein Tipp: Schreibe dir die Grundformel und die umgestellten Formeln einmal alle drei auf dein Blatt, bevor du zu rechnen beginnst. Überlege dir dann, welche Größe du berechnen musst und setze demnach in die jeweilige Formel ein.
4. Fehlerquelle Nummer vier ist besonders ärgerlich. Schüler denken oft nicht daran, dass die Maßeinheiten beim Rechnen einheitlich sein müssen. Wenn du Meter mit Zentimetern, Quadratmeter mir Kubikmetern oder ähnliche Leichtsinnsfehler machst, dann wird dein Ergebnis falsch und das ist besonders dann ärgerlich, wenn die Aufgabe ansonsten richtig gewesen wäre.
Mein Tipp: Suche dir gleich am Anfang einer Aufgabe die sinnvollste Maßeinheit aus und schreibe alle gegebenen Größen in dieser einen Einheit in deine Skizze oder in das Bild in der Aufgabenstellung. Dann kannst du losrechnen, ohne dich nochmal mit den Maßeinheiten beschäftigen zu müssen.
Volumen Prisma: 4 Tipps zur richtigen Berechnung des Volumens eines Prismas:
- Schau dir die Aufgabenstellung genau an. ein Prisma kann manchmal gedreht sein und steht nicht immer auf seiner Grundfläche! Welche Art Grundfläche hast du überhaupt?
- Wenn deine Aufgabenstellung nur ein Text ist, dann fertige dir eine Skizze an und beschrifte sie mit einheitlichen Maßeinheiten. Das erspart dir später eine Menge Arbeit!
- Schreibe dir die Grundformel für das Volumen und auch die beiden Umstellungen zur Berechnung der Grundfläche und der Körperhöhe hin und überlege erst dann, welche Größe du berechnen musst. Was bereits dasteht hilft dir, weil du nicht mehr groß drüber nachdenken musst!
- Rechne das Ergebnis aus und schau insbesondere bei den Maßeinheiten nach, ob es ein sinnvolles Ergebnis sein kann.
Volumen Prisma: Hier bekommst du Hilfestellung
Benötigst du weiterführende, übersichtliche Erklärungen zum Thema Volumen Prisma? Bist du auf der Suche nach weiterem Übungsmaterial?
Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.



Entschuldigung, Kommentare zu diesem Artikel sind nicht möglich.