Volumen Kegel: 5 passende Tipps zum richtigen Berechnen!

Mit Kegeln oder Bowling hat jeder von uns schon mal seinen Abend verbracht. In der Schule musst du jetzt ebenfalls Zeit mit Kegeln verbringen, allerdings jetzt im Bereich der Raumgeometrie und dem Thema Volumen Kegel. Dieser Text wird dir ganz bestimmt dabei helfen. Ich werde dir ausführlich und ohne unwichtige Fachbegriffe erklären, wie du am einfachsten das Volumen eines Kegels berechnest, welche Formeln du brauchst und wie du diese umstellen kannst, um fehlende Größen in Aufgabenstellungen in Klassenarbeiten bestimmen zu können.
Kegel sind wie Pyramiden spitz zulaufende Körper. Spitz zulaufende Körper besitzen eine Grundfläche und die Körperhöhe geht von der Spitze aus senkrecht nach unten. Die Grundfläche eines Kegels ist immer ein Kreis. Im wirklichen Leben sind zum Beispiel die rot-weißen Hütchen an Straßenbaustellen Kegel. Ebenfalls begegnest du ähnlichen Hütchen beim Fußballtraining.
Das Volumen eines Kegels ist eigentlich einfach zu berechnen. Eine Schwierigkeit ist, dass ein Kegel eine zweite Höhe hat, nämlich die Seitenhöhe. Aber schau dir erstmal das folgende Erklärvideo an und wenn du dann noch Fragen hast, dann lies einfach weiter. Ich werde dir übersichtlich erklären, wie du mit der Volumenformel des Kegels rechnen kannst und nenne dir außerdem einige Fehlerquellen, die immer wieder in Klassenarbeiten auftreten.
Volumen Kegel: Erklärvideo
Wie du mit der Volumenformel beim Kegel rechnen musst und wo Fallstricke verborgen sind siehst du im folgenden Erklärvideo.
Volumen Kegel: Welches Grundwissen brauchst du, um das Volumen eines Kegels zu berechnen?
Ein Kegel ist ein spitzer Körper, was wir in der Abbildung oben erkennen können. Deshalb ist die Formel für das Volumen eines Kegels immer die Folgende:
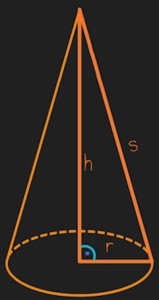
Die Grundfläche eines Kegels ist immer ein Kreis. Die Körperhöhe verläuft immer von der Spitze des Kegels senkrecht auf den Mittelpunkt der kreisförmigen Grundfläche. Dadurch bildet sie zusammen mit dem Radius der Grundfläche einen 90-Grad-Winkel. Das wird später noch wichtig werden, weil ein Kegel zudem immer auch die sogenannte Mantellinie besitzt, zu der man die höhe des Kegels in Beziehung setzen kann.
Aber bleiben wir erstmal bei der Grundfläche, die wie gesagt immer ein Kreis ist. sie besitzt folgende Flächenformel:
Näheres zur Berechnung der Kreisfläche findest du auf der Seite LEARNZEPT.de.
Man kann also die Volumenformel für den Kegel auch ausführlicher schreiben:
Mit dieser Formel kannst du nun das Volumen eines Kegels ausrechnen. In vielen Aufgaben in Klassenarbeiten ist das Volumen jedoch schon gegeben und du musst andere Werte ausrechnen, wie zum Beispiel die Grundfläche oder die Höhe des Kegels. Dazu musst du die Formel so umstellen, dass du auch das gewünschte Ergebnis ausrechnen kannst. Die beiden Formelumstellungen für die Grundfläche und die Höhe habe ich dir hier einmal aufgelistet.
- Grundfläche:
- Höhe:
Manchmal ist es in Klassenarbeiten so, dass du die Höhe des Kegels unter Verwendung der Mantellinie ausrechnen musst. Hier kommt dann der Satz des Pythagoras ins Spiel. Die Grundformel für den Satz des Pythagoras, und weitere ausführliche Erklärungen gibt’s auf der Seite LEARNZEPT.de.
Die Höhe des Kegels und der Radius der Grundfläche bilden gemeinsam mit der Mantellinie ein rechtwinkliges Dreieck, wobei die Mantellinie (hier „s“) die Hypotenuse und der Radius (r) sowie die Höhe (h) die beiden Katheten sind.
Es ergibt sich daraus folgendes Verhältnis:
Jetzt weißt du eigentlich alle Grundlagen um das Thema Volumen Kegel zu meistern. Im Folgenden weise ich dich noch auf ein paar Fehlerquellen hin, die Lehrer in Klassenarbeiten nur zu gerne einbauen, und in die Schüler auch immer wieder hineintappen. Du zum Glück ab heute natürlich nicht mehr.
Volumen Kegel: Diese Fehler machen Schüler immer wieder!
1. Verwechseln der Körperhöhe mit der Mantellinie:
Das Volumen eines Kegels musst du mit der Körperhöhe berechnen. Zur Wiederhlung, die Körperhöhe sagt aus, wie hoch die Spitze des Kegels über dem Mittelpunkt der Grundfläche ist. Sie steht senkrecht auf der Grundfläche! Wenn du diese Höhe nicht gegeben hast, dann musst du sie mithilfe der Mantellinie über den Satz des Pythagoras beziehungsweise das eben dargestellte Verhältnis…
…berechnen!
Mein Tipp: Schau dir die Figur in der Aufgabenstellung genau an und beschrifte sie mit den jeweiligen Maßen. Wenn in der Angabe zur Klassenarbeit keine Zeichnung angegeben ist und die Angaben nur in Textform vor dir liegen, dann mach dir dringend eine Skizze und beschrifte diese.
2. Rechnen mit vermischten Maßeinheiten:
Nicht selten erhalten Schüler falsche Ergebnisse, obwohl sie eigentlich richtig gerechnet haben. Wenn dir das auch schon passiert ist, dann hast du bestimmt in der Aufgabe nicht darauf aufgepasst, dass du mit einheitlichen Maßeinheiten rechnest. Meter darf man nur mit Metern verrechnen und Zentimeter mit Zentimetern usw. Wenn du da nicht aufpasst rechnest du schnell mit den sprichwörtlichen Äpfeln und Birnen und das Ergebnis wird falsch.
Mein Tipp: Beschrifte Zeichnungen und Skizzen gleich so, dass du die Maßeinheiten vereinheitlichst, dann kann dir eine Verwechslung hier schon nicht mehr passieren.
3. Falsche Berechnung der Grundfläche:
Die Grundfläche eines Kreises ist immer ein heißer Kandidat für Fehler in Klassenarbeiten. Schüler verwechseln hier nämlich gerne den Kreisumfang mit der Kreisfläche. Wenn du das Volumen aber mit der Formel für den Kreisumfang rechnen willst, dann kommt dabei natürlich Mist heraus.
Mein Tipp: Denke daran, dass die Kreisfläche mit der folgenden Formel ausgerechnet wird:
Wiederholen kannst du die Flächenformel am Kreis und ihre richtige Anwendung auf der Seite LEARNZEPT.de.
4. Falsches Umstellen der Volumenformel:
Wie bereits weiter oben erwähnt, ist es in Klassenarbeiten oft so, dass du das Volumen gegeben hast und entweder die Grundfläche oder die Höhe des Kegels berechnen musst. Hier machen Schüler oft Fehler beim Umstellen der Volumenformel.
Mein Tipp: Schreibe dir die Umstellungen der Volumenformel je nach Ergebnis, das du berechnen sollst gleich zu Beginn der Aufgabe auf, dann brauchst du’s nur noch abschreiben, wenn du Werte einsetzen musst und kannst dich voll darauf konzentrieren. Hier nochmal die beiden Formelumstellungen:
Grundfläche:
Höhe:
Tipps und Tricks zum Umstellen von Formeln bietet dir die Seite LEARNZEPT.de.
Volumen Kegel: 5 zusammenfassende Tipps:
- Beschrifte die Figur in der Angabe der Klassenarbeit mit den richtigen Maßeinheiten! Wenn du keine vorgegebene Zeichnung hast, dann fertige dir unbedingt eine Skizze an und beschrifte diese! Achtung: Passe gleich zu Beginn die Maßeinheiten an!
- Schreibe dir die Formeln, die du für die Volumenberechnung beim Kegel brauchst auf! Denke an die Abwandlungen wenn du die Höhe oder die Grundfläche berechnen sollst!
- Prüfe in der Angabe der Klassenarbeit ganz genau, welche Größen du gegeben hast! Verwechsle nicht die Mantellinie mit der Höhe des Kegels!
- Setze die gegebenen Maße in deine Formeln ein! Vergewissere dich nochmal, ob du auch wirklich die Maßeinheiten angeglichen hast!
- Prüfe, ob dein Ergebnis sinnvoll ist und stimmen kann. (Denke daran, dass man das Volumen in Kubikmetern bzw. Kubikzentimetern misst. Das bedeutet „hoch 3“!)
Volumen Kegel: Hier bekommst du Hilfestellung
Wie wäre es, wenn du das Thema Volumen Kegel übersichtlich und leicht verständlich wiederholen könntest?
Möchtest du mit echten Klassenarbeiten und ausführlichen Erklärungen und Lösungen auf die nächste Prüfung lernen?
Erklärvideos und echte, interaktiv aufbereitete Klassenarbeiten zur Übung gibt’s nur auf der Online-Lernplattform Learnzept! Klicke hier für einen kostenlosen Account!


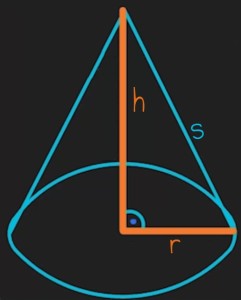

Entschuldigung, Kommentare zu diesem Artikel sind nicht möglich.