Volumen Pyramide: 6 Tipps zur Berechnung des Volumens

Wie berechnet man unkompliziert das Volumen von Pyramiden? Welche Formeln braucht man und wie stellt man sie um, wenn wir eine Größe berechnen müssen, wie die Grundfläche, die Körperhöhe oder die Seitenhöhe? Wann muss man mit dem Satz des Pythagoras arbeiten? Alle diese Fragen werden wir jetzt gemeinsam klären.

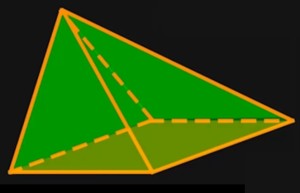
Pyramiden sind nicht nur beliebte Ausflugsziele in Ägypten sondern auch wichtige geometrische Körper innerhalb der Raumgeometrie. Innerhalb der Raumgeometrie gibt es gerade Körper und spitz zulaufende Körper. Letzeres sind alle Pyramiden. Spitz zulaufend heißt, es gibt nur eine Grundfläche. Außerdem hat eine Pyramide vier Seitenhöhen, vier Kanten und eine Körperhöhe.

Alle diese Eigenschaften können für das Thema Volumen Pyramide je nach Aufgabenstellung von Bedeutung sein. Das klingt jetzt zwar unheimlich kompliziert und man muss schon festhalten, dass Pyramiden nicht die einfachsten Körper zur Berechnung sind. Aber wir kriegen das trotzdem in den Griff. Wir werden uns so verständlich wie möglich mit dem Grundwissen auseinandersetzen, das du brauchst, um das Volumen einer Pyramide auszurechnen und uns auch ausführlich die häufigsten Fehlerquellen ansehen.

Volumen Pyramide: Erklärvideo

Im folgenden Erklärvideo gibt es ausführliche Erklärungen zu allen Problemstellungen des Themas Volumen Pyramide.

Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren

Video laden

YouTube immer entsperren

Volumen Pyramide: Was musst du zur Volumenberechnung wissen?

Wir haben bereits festgestellt, dass Pyramiden spitz zulaufende Körper sind. Das sehen wir auch an der Abbildung oben. Diese Information führt uns zur Volumenformel, die für alle Pyramiden gültig ist:

$V \quad = \quad \frac{1}{{3}} \quad \cdot \quad A_{{G}} \quad \cdot \quad h$

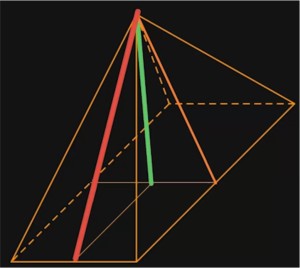
A ist dabei die Grundfläche und h die Höhe der Pyramide. Die Grundfläche einer Pyramide kann aus Rechtecken, Quadraten oder auch Dreiecken bestehen. Wenn du die Berechnung verschiedener Grundflächen noch einmal wiederholen möchtest, findest du auf der Seite LEARNZEPT.de ausführliche Tipps und Tricks. Die Höhe einer Pyramide bemisst sich immer von ihrer Spitze senkrecht auf die Grundfläche. Eine Pyramide besitzt nämlich noch weitere Höhen, die von der Körperhöhe unterschieden werden müssen. Diese sind nämlich die Höhen der Dreiecke, die zusammen die Mantelfläche der Pyramide bilden.

Jetzt können wir schonmal das Volumen anhand der Formel ausrechnen. Wenn wir jetzt das Volumen gegeben haben und stattdessen eine der beiden anderen Größen der Pyramide (Höhe / Grundfläche) ausrechnen wollen, dann müssen wir nur die Formel umstellen um das gewünschte Ergebnis zu erhalten.

Grundfläche: $A_{G} \quad = \quad 3 \quad \cdot \quad \frac{V}{h}$
Höhe: $h\quad = \quad 3 \quad \cdot \quad \frac{V}{A_{G}}$

Mit den beiden Umstellungen der Volumenformel können wir jetzt also die Körperhöhe und die Grundfläche berechnen.

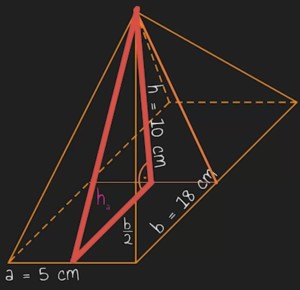
Was bei der Pyramide etwas knifflig ist, wenn wir die Körperhöhe nicht gegeben haben, sie aber benötigen, um das Volumen der Pyramide zu berechnen. Zumeist haben wir in diesem Fall aber eine der Seitenhöhen der Seitenflächen gegeben. Mit diesen können wir, da der Winkel am Fußpunkt der Pyramide immer ein 90-Grad-Winkel ist, die Körperhöhe ausrechnen. Wir tun dies mit dem Satz des Pythagoras:

$a^{2} \quad + \quad b^{2} \quad = \quad c^{2}$

Wie du den Satz des Pythagoras richtig verwendest siehst du dir am besten auf der Seite LEARNZEPT.de genauer an.

Die Körperhöhe ist dabei immer eine Kathete und die Höhe des Seitendreiecks immer die Hypothenuse. Wenn du jetzt weißt, wie hoch die Pyramide ist, dann kannst du wieder bequem mit der Volumenformel von eben und ihren Umstellungen rechnen.

Volumen Pyramide: Diese Fehler machen Schüler immer wieder!

Beim Thema Volumen Pyramide kann man an drei Stellen Fehler machen.

Verwechseln von Körperhöhe und Seitenhöhe:
Die wichtigste und häufigste Fehlerquelle ist, dass Schüler die Körperhöhe mit der Höhe der Dreiecke des Mantels verwechseln. Mit der Seitenhöhe können wir nicht das Volumen der Pyramide ausrechnen, wohl aber die Körperhöhe mithilfe des Satzes des Pythagoras.
Tipps zur richtigen Anwendung des Satzes des Pythagoras findest du, wie bereits erwähnt, auf der Seite LEARNZEPT.de.
Mein Tipp: Schau dir die Figur in der Aufgabenstellung genau an und beschrifte sie mit den jeweiligen Maßen. Wenn in der Angabe zur Klassenarbeit keine Zeichnung angegeben ist und die Angaben nur in Textform vor dir liegen, dann mach dir dringend eine Skizze und beschrifte diese.
Maßeinheiten werden nicht angeglichen:
Beim Beschriften einer Skizze musst du darauf achten, dass du die Maßeinheiten genau hinschreibst. Du darfst nämlich nur mit gleichen Maßeinheiten rechnen, das heißt nur mit Zentimetern (cm) oder Metern (m) usw. Oft haben Schüler sich schon die Note einer Klassenarbeit dadurch verdorben, weil sie ohne darauf zu achten in der gleichen Aufgabe Meter, Zentimeter oder Millimeter einfach zusammengezählt haben. Nicht machen! Wie war das mit den Äpfeln und den Birnen?
Mein Tipp: Entscheide dich gleich zu Beginn für eine Maßeinheit, die sinnvoll ist und wandle alle anderen Maßeinheiten in diese um!
Falsche Umstellung der Volumenformel:
Immer wieder passiert es Schülern, dass sie die Volumenformel falsch umstellen, wenn andere Größen, wie die Grundfläche und die Körperhöhe gesucht sind. Wie du Formeln richtig umstellen kannst wird dir auch ausführlich auf der Seite LEARNZEPT.de vorgeführt.
Mein Tipp: Die drei Formeln am besten auswendig lernen. Hier stehen sie nochmal:
$V \quad = \quad \frac{1}{{3}} \quad \cdot \quad A_{{G}} \quad \cdot \quad h$
$A_{G} \quad = \quad 3 \quad \cdot \quad \frac{V}{h}$
$h\quad = \quad 3 \quad \cdot \quad \frac{V}{A_{G}}$

Volumen Pyramide: Abschließend 6 Tipps zur richtigen Volumenberechnung!

Die Figur in der Angabe der Klassenarbeit genau beschriften. Wenn nötig zeichne dir eine Skizze und beschrifte diese.
Schreibe nach der Skizze alle drei Formeln zur Volumenberechnung einer Pyramide auf, damit du dann gleich die zur Hand hast, die du brauchst.
Gleiche gleich zu Beginn die Maßeinheiten an!
Schau genau hin, welche Maßeinheiten gegeben sind und welche du berechnen sollst. Achtung: Seitenhöhe und Körperhöhe sind zwei paar verschiedene Stiefel. Zur Volumenberechnung brauchst du die Körperhöhe. Eventuell musst du sie mit dem Satz des Pythagoras ausrechnen.
Setze die Maßeinheiten, die du gegeben hast in die jeweilige Formel ein, je nachdem, welche Größe der Pyramide du berechnen musst.
Überprüfe dein Ergebnis, ob es sinnvoll ist und die richtige Maßeinheit dahintersteht. (Volumen misst man in Kubikmetern, Kubikzentimetern usw.! Nicht das „hoch 3“ vergessen! Auf solche Leichtsinnsfehler warten böse Lehrer nur!)

Volumen Pyramide: Hier bekommst du Hilfestellung

Benötigst du weiterführende, übersichtliche Erklärungen zum Thema Volumen Pyramide? Bist du auf der Suche nach weiterem Übungsmaterial?

Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.

(2 Bewertung/en, durchschnittlich: 3,00 von 5)