Mittelsenkrechte: 6 Tipps zu Bedeutung und Konstruktion

Die Mittelsenkrechte ist ein geometrischer Ort. Sie hat deswegen spezielle Eigenschaften, über die man die Lage von anderen Punkten in der Geometrie bestimmen kann. Diese speziellen Eigenschaften werde ich dir in diesem Text übersichtlich und ohne unnötige Fachbegriffe erklären. Außerdem kann man die Mittelsenkrechte auch konstruieren. Wie das mit Zirkel und Geodreieck am einfachsten funktioniert werde ich dir auch erklären. Danach beherrscht du das Thema Mittelsenkrechte perfekt und hast damit in Klassenarbeiten keine Schwierigkeiten mehr.

Lass uns das Wort Mittelsenkrechte mal in zwei Teile aufteilen.

Da hätten wir zum einen „mittel-„. Offensichtlich liegt die Mittelsenkrechte genau in der Mitte von irgendetwas. Die Mittelsenkrechte liegt in der Mitte zwischen zwei Punkten oder zwei Halbebenen. Dazu später mehr.

Zum anderen haben wir noch den Teil „-senkrechte“. Das verrät uns, dass die Mittelsenkrechte zu irgendetwas senkrecht steht, damit also einen 90-Grad-Winkel bildet. Sie tut die auf der kürzesten Verbindung zwischen den beiden Punkten zwischen denen sie in der Mitte liegt.

Püh! Ganz schön kompliziert, nicht? Aber das klingt nur so. Schau dir zunächst einmal das folgende Video an. Danach sollten sich deine Sorgenfalten auf der Stirn schon etwas gemildert haben. Wenn nicht und du brauchst noch weitere Erklärungen zum Thema Mittelsenkrechte, dann ließ einfach im Text  weiter.
 
 

 
 

Was ist wichtig? Was musst du wissen?

Geometrische Bedeutung der Mittelsenkrechten

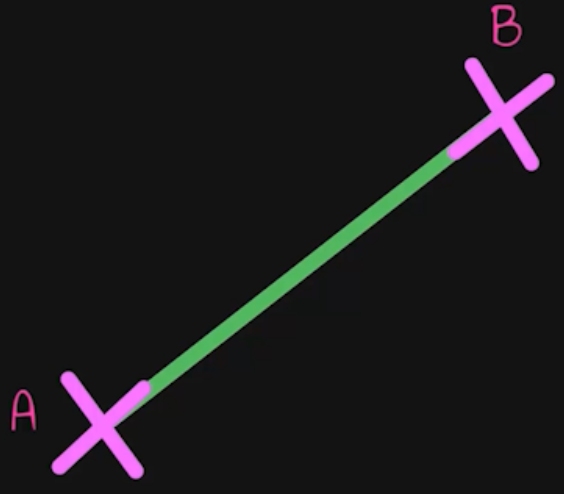
Gehen wir zum Thema Mittelsenkrechte zunächst davon aus, dass wir zwei Punkte haben, die durch eine Linie verbunden sind.

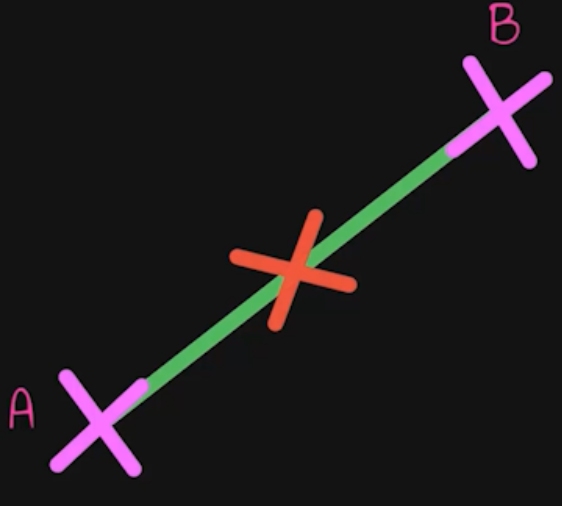
Zwischen diesen beiden Punkten suchen wir uns nun die Mitte.

Wenn du in diesem Mittelpunkt einen 90-Grad-Winkel anlegst und eine Gerade ziehst, dann erhältst du eine Gerade, auf der alle Punkte liegen, die von den Punkten A und B gleichweit entfernt sind. Diese Gerade heißt dann Mittelsenkrechte. An folgender Skizze erkennst du nun die geometrische Bedeutung der Mittelsenkrechte deutlich.

Wir fassen die geometrische Bedeutung der Mittelsenkrechte nochmal zusammen:

Die Mittelsenkrechte ist eine Gerade, die senkrecht (90-Grad-Winkel) durch den Mittelpunkt auf einer Strecke zwischen zwei Punkten A und B liegt. Damit bildet diese Mittelsenkrechte die Menge aller Punkte, die von A und B genau gleich weit entfernt sind.

Zusätzlich dazu, dass die Mittelsenkrechte die Menge aller Punkte ist, die von A und B gleich weit entfernt sind, weißt du auch, dass alle Punkte rechts der Geraden näher an B als an A liegen. Dadurch definiert die Mittelsenkrechte rechts und links von sich selbst jeweils eine Halbebene in der alle Punkte näher bei einem der beiden Punkte A und B liegen.

Eine genauere Erklärung der Halbebenen findest du auf der Seite LEARNZEPT.de.

 

Konstruktion der Mittelsenkrechten

Zur Konstruktion der Mittelsenkrechten gehen wir noch einmal von unserer Strecke zwischen den Punkten A und B aus. Zu dieser wollen wir die Mittelsenkrechte konstruieren. Du gehst am besten in den folgenden Schritten vor.

1. Zeichne dir die Strecke, zu der du die Mittelsenkrechte konstruieren willst auf und markiere die Punkte A und B.
2. Ziehe um den Punkt A einen Halbkreis. Der Radius muss größer sein als die Hälfte der Strecke zwischen A und B.
   
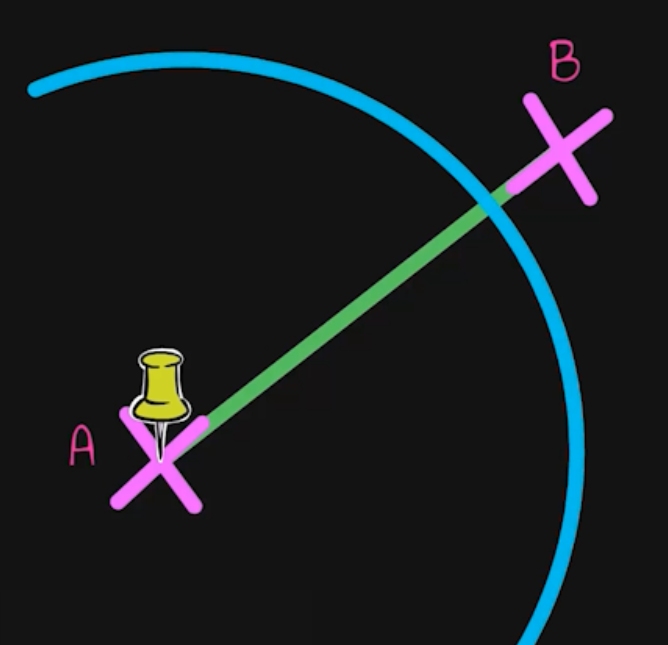
3. Ziehe den gleichen Halbkreis nur in anderer Richtung um B.
   Es ist wichtig, dass beide Kreise um die Punkte den gleichen Radius haben!
4. Markiere die Schnittpunkte der beiden Halbkreise und verbinde sie.
   

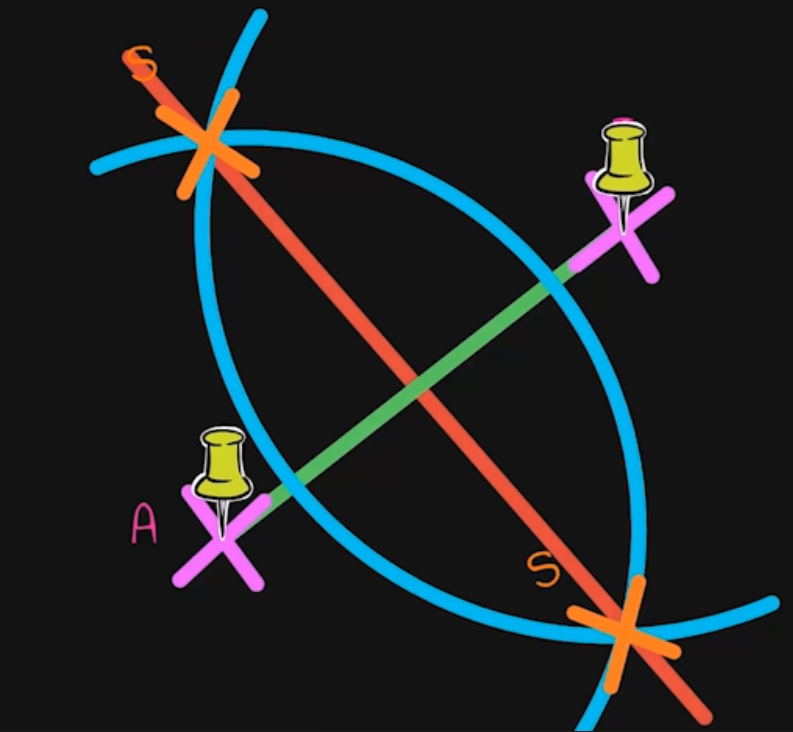
Fertig: Du hast die Mittelsenkrechte konstruiert!

Tipps und Tricks zur Konstruktion anderer geometrischer Orte wie der Winkelhalbierenden u.ä. gibt’s auf LEARNZEPT.de.

 

Mittelsenkrechte: Die häufigsten Schülerfehler zusammengefasst

Fehler kannst du bei diesem Thema eigentlich nur bei der Konstruktion der Mittelsenkrechten machen. Die Eigenschaften musst du dir anschauen, versuchen zu verstehen und dann lernen.

 

Fehler bei der Konstruktion

1. Der Radius, den du um die beiden Punkte A und B (siehe Skizze oben) ziehen musst, muss so gewählt sein, dass er größer ist als die Hälfte der Strecke zwischen den beiden Punkten. Oft behaupten Schüler nämlich es „gäbe keinen Schnittpunkt“, dabei haben sie den Radius nur zu klein gewählt.Mein Tipp: Nimm als Radius einfach die gesamte Länge der Strecke zwischen A und B, dann bist du auf der sicheren Seite.
2. Schüler verwenden für die beiden Halbkreise oft nicht den gleichen Radius. Das ist natürlich auch falsch. Auf diese At und Weise erhältst du vielleicht zwei Schnittpunkte und eine Gerade, aber nie und nimmer die Mittelsenkrechte.Mein Tipp: Auch hier kann ich dir nur den Tipp geben, als Radius einfach immer den Abstand zwischen den Punkten A und B zu verwenden.

 

In 6 Tipps das Wichtigste zusammengefasst

Geometrische Bedeutung

1. Die Mittelsenkrechte heißt Mittelsenkrechte, weil sie eine Gerade ist, die im 90-Grad-Winkel ( = rechter Winkel / = senkrecht) eine Strecke genau in deren Mitte schneidet.
2. Die Mittelsenkrechte zwischen den Punkten A und B ist die Menge der Punkte, die von den beiden Punkten A und B genau gleichweit entfernt sind.
3. Links und rechts von der Mittelsenkrechte sind alle Punkte, die jeweils näher an einem der beiden Punkte A und B liegen. ( = Halbebene)

 

Konstruktion

1. Ziehe Halbkreise um die beiden Endpunkte der Strecke, deren Mittelsenkrechte du konstruieren möchtest.
   (Achtung Radius!!!)
2. Verbinde die Schnittpunkte der beiden Halbkreise
3. Überprüfe deine Zeichnung: Ist der Schnittwinkel von Strecke und Mittelsenkrechte wirklich 90 Grad?

 

Hier bekommst du Hilfestellung:

Benötigst du weiterführende, übersichtliche Erklärungen zum Thema Mittelsenkrechte? Bist du auf der Suche nach weiterem Übungsmaterial?

Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.

(5 Bewertung/en, durchschnittlich: 4,00 von 5)

Loading...