Wechselwinkel: 3 Tipps zum besseren Verständnis

Winkel werden oft in der Geometrie zueinander in Beziehung gesetzt, um unbekannte Winkel in einer Figur auszurechnen. Aus diesem Grund beschäftigst du dich im Mathematikunterricht in der Mittelstufe auch mit den sogenannten Wechselwinkeln. Was aber sind Wechselwinkel und welche Eigenschaften haben sie? Diesen Fragen werden wir im Folgenden Text nachgehen und feststellen, dass Wechselwinkel sehr einfach zu verstehen sind und eine große Hilfe für dich sind, wenn du ihre Eigenschaften verstanden hast. Los geht’s!

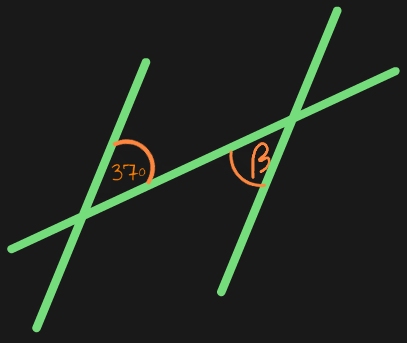
Wechselwinkel findest du immer dann, wenn du in einer Aufgabenstellung zwei parallele Geraden gegeben hast, die von einer dritten Geraden beliebig geschnitten werden. Folgende Skizze zeigt dir, wie ein mögliches Bild aussehen kann, bei dem du die Wechselwinkel anwenden kannst.

Du erkennst die beiden parallelen Geraden, die von einer dritten Geraden geschnitten werden. Die beiden angegebenen Winkel sind Wechselwinkel.

Welche speziellen Eigenschaften musst du kennen?

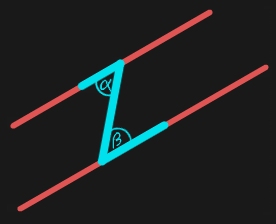
Wechselwinkel findet man an den Schnittstellen, an denen zwei parallele Geraden von einer dritten Geraden geschnitten werden. Sie liegen einander in Form des Buchstaben „Z“ gegenüber und deshalb werden sie auch oft „Z-Winkel“ genannt. Die folgende Skizze macht dies für dich bestimmt leicht verständlich.

Diese beiden Winkel α und β liegen wie gesagt einander gegenüber. Sie haben die Eigenschaft, dass sie immer gleich groß sind oder mathematisch ausgedrückt:

$\alpha \quad = \quad \beta$

Man kann also zwei Aussagen bezüglich der Wechselwinkel treffen:

Werden zwei parallele Geraden von einer dritten Geraden geschnitten, dann sind die Wechselwinkel α und β gleich groß.
Findet man, wenn zwei Geraden von einer Dritten geschnitten werden zwei gleich große Wechselwinkel, dann sind die beiden ersten Geraden immer parallel.

Ausführliche Erklärungen zu anderen Winkeln wie Stufenwinkel, Scheitelwinkel und Nebenwinkel findest du auf der Seite LEARNZEPT.de.

Fehlerquelle! Wie erkennst du Wechselwinkel?

Sicherlich ist es dir auch schon so ergangen: Du kommst in einer Aufgabe nicht weiter und bei der Korrektur kommt der schlaue Lehrer und sagt, du hättest doch einfach bloß die Wechselwinkel erkennen müssen.

Da meine Unterrichtserfahrung aber zeigt, dass Schüler diese Winkel oft nicht erkennen, kann es wohl auch nicht so einfach sein. Einige Erkennungsmerkmale liste ich dir hier auf:

Wir brauchen zwei parallele Geraden.
Wir brauchen außerdem eine dritte Gerade, die die beiden Parallelen in einem bestimmten Winkel schneidet.
Die beiden Parallelen und die Schnittgerade müssen in ihren Schnittpunkten den Buchstaben „Z“ nachvollziehen. (Siehe hierfür noch einmal die beiden Skizzen oben!)
Wechselwinkel liegen einander gegenüber.

Mein Tipp: Suche in einer solchen Aufgabe einfach nach Möglichkeiten, den Buchstaben „Z“ zu bilden und male ihn mit einem Markierstift nach. Die Winkel, die dann einander in diesem „Z“ gegenüber liegen müssen dann gleich groß sein. Miss es mit dem Geodreieck zur Sicherheit einmal nach.

Wechselwinkel: 3 Tipps zum Erkennen und zur Verwendung ihrer Eigenschaften

Schau dir die angegebene Zeichnung genau an und suche den Buchstaben „Z“!
Wenn du keine Zeichnung gegeben hast, dann mach dir eine Skizze.
Wechselwinkel liegen einander gegenüber und sind gleich groß.
(Vergewissere dich mit dem Geodreieck!)
Hast du zwei Wechselwinkel gefunden, dann weißt du gleichzeitig, dass die beiden Geraden, die vor der Dritten geschnitten werden parallel sind!

Wechselwinkel: Hier bekommst du Hilfestellung

Wie wäre es, wenn du die Eigenschaften der Wechselwinkel und ihre Verwendung übersichtlich und leicht verständlich wiederholen könntest? Möchtest du mit echten Klassenarbeiten und ausführlichen Erklärungen und Lösungen auf die nächste Prüfung lernen?

Erklärvideos und echte, interaktiv aufbereitete Klassenarbeiten zur Übung gibt’s nur auf der Online-Lernplattform Learnzept! Klicke hier für einen kostenlosen Account!

(7 Bewertung/en, durchschnittlich: 4,14 von 5)