Sinussatz: 3 Tipps zur korrekten Verwendung

Im rechtwinkligen Dreieck bist du bereits Experte und weißt genau wie du unterschiedliche Größen wie Winkel und Seitenlängen berechnen kannst. Bestimmte Winkelverhältnisse wie „sinα = Gegenkathete / Hypotenuse“, „cosα = Ankathete / Hypotenuse“ oder „tanα = Gegenkathete / Ankathete“ kennst du auch schon und in der Verwendung des Satzes des Pythagoras hast du auch keine Schwierigkeiten. Jetzt stellt sich allerdings die Frage, wie du Größe in nicht-rechtwinkligen Dreiecken berechnen kannst. Dafür gibt es den Sinussatz. Hier lernst du was der Sinussatz ist und wie du ihn anwenden kannst.
Der Sinussatz ist denkbar einfach. Wir schreiben ihn uns einfach mal hin:
Wenn du also die Länge einer Seite durch den Sinus des gegenüberliegenden Winkels teilst, kommt immer das selbe Ergebnis heraus.
Wenn in deinem Dreieck also mindestens drei Größen gegeben sind und ein „Seiten-Winkel-Paar“ dabei ist, kannst du den Sinussatz verwenden, um die anderen Größen zu berechnen.
Solltest du aber nur die drei Seiten gegeben haben oder aber zwei Seiten und den eingeschlossenen Winkel so, so hilft dir der Sinussatz NICHT weiter und du brauchst den Kosinussatz.
Schau dir zuerst einmal das folgende Video an. In ihm werden dir die Bedeutung und die Verwendung des Sinussatzes ausführlich erklärt. Wenn du danach noch Fragen hast, lies einfach an dieser Stelle im Text weiter.
Sinussatz: Erklärvideo
Sinussatz: Grundwissen, das du für die Verwendung benötigst
Wie wende ich den Sinussatz richtig an?
Als erstes sollte dir auffallen, dass in der Formel zwei Gleichheitszeichen vorkommen. Eines reicht aber bereits. Wir müssen also nie die ganze Formel benutzen. Je nach dem was gegeben ist kann es auch sinnvoll sein die Formel umzustellen. Zum Beispiel so:
Oder auch so:
Oder ebenfalls möglich:
Es gibt auch noch weitere Möglichkeiten, zunächst wollen wir es jedoch dabei belassen.
Woher weiß ich, welche Variante ich nehmen soll?
Anstatt all die Umformungen auswendig zu lernen empfehle ich dir, dir eine Skizze zu machen! In der Geometrie solltest du dir immer eine Skizze machen, aber hier ganz besonders. Du musst auch kein Bild malen. Eine grobe Skizze reicht aus.
Eine häufige Fehlerquelle ist das Verwenden der falschen Formel und Fehler beim Umstellen. Um dies zu vermeiden empfehle ich dir ein starres Schema. Auch wenn da dann manches etwas umständlich ist, so vermeidet es doch viele Fehler in Klassenarbeiten.
Welches Schema du dabei verwendest, hängt von dir oder deinem Lehrer ab. Die einen machen es so, die andern so. Am Ende musst aber du die Aufgabe lösen. Also schau dir die beiden Schemata an und überlege dir, welches dir besser gefällt. Nur vermische sie bitte nicht. Entscheide dich für eines.
Als Alternative zum Schema aus dem Video empfehle ich dir, in deiner Skizze alle bekannten und gesuchten Größen einzutragen. Verbinde gegenüberliegende Seiten und Winkel die gegeben sind z.B mit Grün. Dieses Paar benutzt du als „Referenz“. Verwende am besten immer die gleichen Farben, damit du dich daran gewöhnst.
Markiere dir eine gesuchte Größe zum Beispiel in Lila, aber bedenke, die gegenüberliegende Größe muss gegeben sein.
Schreibe die gesuchte Größe in den Zähler und die gegenüberliegende in den Nenner. Auf die rechte Seite deines Gleichheitszeichens schreibst du dann dein Referenzpaar. Achte darauf, dass wenn auf der linken Seite der Winkel im Zähler steht, er das auf der rechten Seite auch muss. Gleiches gilt, wenn links die Seite im Zähler steht, dann muss sie dort auch auf der rechten Seite stehen.
Hast du jetzt alles richtig gemacht, dann löst du nach der gesuchten Größe auf, indem du die Gleichung mit dem linken Nenner multiplizierst. Dann bestimmst du die gesuchte Größe.
Das machst du solange, bis du alles bestimmt hast, was du wissen möchtest.
Fehlt dir ein „Paar“ aus Seite und gegenüberliegendem Winkel komplett, dann kannst du den Winkel mit der Winkelsumme im Dreieck berechnen.
Das alles in einem Beispiel:
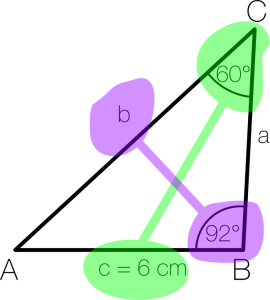
Vom Dreieck ABC sind a = 10cm, b = 13cm und β = 122° gegeben!
Referenzpaar finden:
Du erkennst, dass b und β gegeben sind. Diese beiden Werte sind dein Referenzpaar.
Gesuchte Größe in den Zähler schreiben:
Da a auch gegeben ist, suchst du als erstes α. Da wir α suchen, schreiben wir sinα in den Zähler. Darum muss a dann in den Nenner.
Mit Referenzpaar gleichsetzen:
Dein Referenzpaar war b und β. Da sinα im linken Zähler steht, schreibst du auch sinβ in den Zähler und b dann in den Nenner. Als Gleichung erhältst du so recht schnell:
Bekannte Werte einsetzen:
Gleichung nach gesuchter Größe umstellen und lösen.
Jetzt gibst du die rechte Seite in den Taschenrechner ein. Dieser liefert dir folgendes Ergebnis: sinα = 0,6523.
Daraus folgt: α = 40,7°
Jetzt kennst du also a = 10cm, b = 13cm, sinβ = 122°, α = 40,7°
Es fehlen dir jetzt noch c und γ. Hier hilft dir der Sinussatz nicht weiter, da dir das Referenzpaar aus c und γ fehlt. Du brauchst eine andere Möglichkeit um auf c oder auf γ zu kommen. Du kennst die Winkelsumme im Dreieck, und weißt daher, dass α + β + γ = 180°. Das nutzt du jetzt natürlich zur Berechnung von γ aus. 40,7° + 122° + γ = 180°. Aus dieser Rechnung ergibt sich, dass γ = 17,3°.
Wenn du im Thema „Winkelsumme im Dreieck“ nicht mehr topfit bist, dann gibt’s Trainingsmaterial dazu auf der Seite LEARNZEPT.de.
Jetzt kannst du mit dem Sinussatz c berechnen. Also zurück zum Anfang:
Referenzpaar finden:
Als Referenzpaar kannst du immer noch b und β nehmen.
Gesuchte Größe in den Zähler schreiben:
Gerade hast du ja γ ausgerechnet. Wenn γ bekannt ist, dann suchen wir c und schreiben c daher in den Zähler, γ dagegen wandert in den Nenner.
Mit Referenzpaar gleichsetzen:
Dein Referenzpaar war b und β. Da c im linken Zähler steht, schreibst du auch b in den Zähler und sinβ dann in den Nenner. Als Gleichung erhältst du so recht schnell:
Du siehst, dass hier die Seiten im Zähler sind. Das ist gut, da wir ja eine Seite suchen.
Bekannte Werte einsetzen:
Gleichung nach gesuchter Größe umstellen und lösen:
Der Taschenrechner verrät dir jetzt das c = 4,56cm. Damit hast du alle Seiten und Winkel bestimmt.
Sinussatz: Diese Fehler solltest du vermeiden!
- Oft schreiben Schüler die gesuchte Größe in den Nenner. Das ist zwar erst einmal nicht falsch, ist aber so schwer umzustellen, dass dabei fast zwangsläufig Fehler passieren.
Daher mein Tipp: Schreibe das, was du suchst immer in den Zähler. Beim Sinussatz geht das!
- Viele Schüler verwechseln den Sinus mit dem Sinussatz. Der Sinus ist nur im rechtwinkligen Dreieck definiert als Gegenkathete geteilt durch Hypotenuse.
(Ausführliche Informationen und Übungsmaterial zum Sinus im rechtwinkligen Dreieck findest du auf der Seite LEARNZEPT.de.)
Der Sinussatz hingegen gilt in einem beliebigen Dreieck. Allerdings müssen hier drei Größen gegeben sein, um die Vierte ausrechnen zu können.
Sinussatz: Das Wichtigste in 3 Tipps
- Markiere dir das Seiten-Winkel-Paar das vollständig gegeben ist. Es ist dann dein Referenzpaar.
- Schreibe die gesuchte Größe in den Zähler und die zugehörige gegenüberliegende Größe in den Nenner. Schreibe die Referenz auf die rechte Seite. Achte darauf, dass Seite und Winkel analog zur linken Seite im Zähler und Nenner stehen.
- Stelle die Gleichung nach der gesuchten Größe um.
Sinussatz: Hier erhältst du Hilfestellung
Benötigst du weiterführende, übersichtliche Erklärungen zum Thema Sinus Satz? Bist du auf der Suche nach weiterem Übungsmaterial?
Die Online-Lernplattform Learnzept bietet dir zu diesem Thema ausführliche Erklärvideos und echte Klassenarbeiten interaktiv aufbereitet. Klicke hier für einen kostenlosen Zugang.

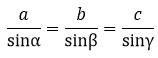

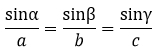
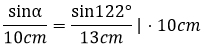

 (5 Bewertung/en, durchschnittlich: 4,40 von 5)
(5 Bewertung/en, durchschnittlich: 4,40 von 5)
Entschuldigung, Kommentare zu diesem Artikel sind nicht möglich.